니티놀은 대개 유한 변형을 받는 경우에 사용되므로 대수 변형 및 대단위 및 업데이트된 라그랑주 공식을 활용하는 변형 공식이 이 모델에 사용됩니다.
따라서 대수 변형과 Kirchhoff 응력 부품이 관련되는 구성 모델이 만들어집니다. 그러나 최종적으로 구성 매트릭스와 응력 벡터는 모두 코쉬 응력(실제 크기)으로 변형되어 표시됩니다.
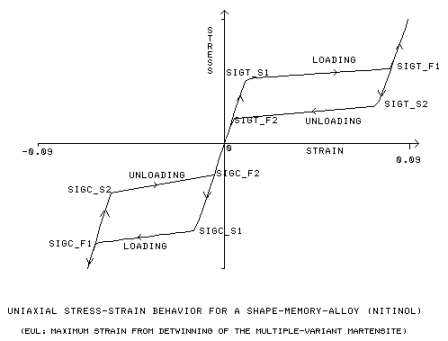
|
σs
t1, σf
t1
|
인장 하중 부가를 위한 초기 및 최종 항복 응력 [SIGT_S1, SIGT_F1]
|
|
σs
t2, σf
t2
|
인장 하중 제거를 위한 초기 및 최종 항복 응력 [SIGT_S2, SIGT_F2]
|
|
σs
c1, σf
c1
|
압축 하중 부가를 위한 초기 및 최종 항복 응력 [SIGC_S1, SIGC_F1]
|
|
σs
c2, σf
c2
|
압축 하중 제거를 위한 초기 및 최종 항복 응력 [SIGC_S2, SIGC_F2]
|
|
eul
|
(최대 소성 인장 응력) *(3/2)0.5
|
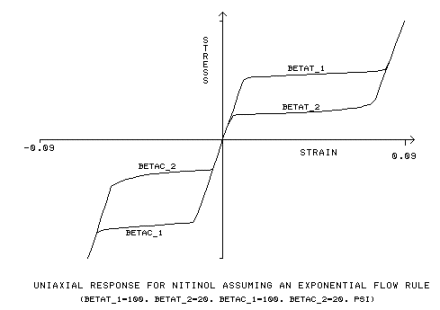
지수 유동률 규칙에서는 추가 입력 상수 β
t1, β
t2, β
c1, β
c2를 사용합니다.
|
βT1 값
|
인장 하중 부가의 변형 속도를 측정하는 재질 파라미터, [BETAT_1]
|
|
βT2 값
|
인장 하중 제거의 변형 속도를 측정하는 재질 파라미터, [BETAT_2]
|
|
βc1
|
압축 하중 부가의 변형 속도를 측정하는 재질 파라미터, [BETAC_1]
|
|
βc2
|
압축 하중 제거의 변형 속도를 측정하는 재질 파라미터, [BETAC_2]
|
항복 기준
단계 변형의 압력 의존 가능성을 모델링하기 위해 Drucker-Prager 유형 하중 부가 함수를 항복 기준에 사용합니다.
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RI
f = 0
여기에서
σ(bar) = 유효 응력
p = 평균 응력(또는 정수압)
α = sqrt(2/3) (σsc1 - σst1) / (σsc1 + σst1)
Rf
I = [ σf
I(sqrt(2/3) + α)], I = 1(하중 부가) 및 2(하중 제거)