Amplituda naprężenia przemiennego dla cyklu naprężenia jest obliczana jako połowa zakresu naprężenia w cyklu. Ilość uszkodzenia spowodowanego przez cykl naprężenia zależy nie tylko od naprężenia przemiennego, ale również od naprężenia średniego. Na przykład: dwa niżej przedstawione cykle posiadają to samo naprężenie przemienne, jednakże powodują różne ilości uszkodzenia, ponieważ posiadają różne naprężenia średnie.
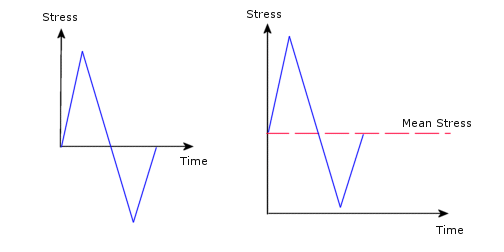
Wpływ naprężeń średnich na liczbę cykli, która powoduje zniszczenie przedstawiony został na poniższym diagramie, zwanym diagramem Haigha.
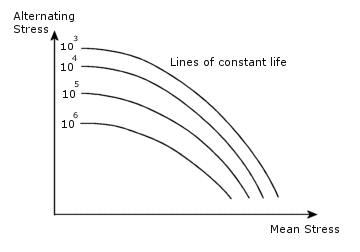
Naprężenie średnie jest zerowe tylko wtedy, gdy obciążenie jest całkowicie odwracalne. Najprostszy przypadek jest wtedy, gdy dostarczono krzywą S-N o takim samym współczynniku R jak obciążenie. W tym przypadku krzywa S-N jest wykorzystywana bezpośrednio, ponieważ nie jest wymagana żadna korekta. Jeżeli zdefiniowano krzywe S-N o różnych współczynnikach R, to oprogramowanie uwzględni naprężenie średnie poprzez dokonanie interpolacji liniowej pomiędzy krzywymi. Jeżeli dostarczona jest tylko jedna krzywa S-N o współczynniku R różnym od współczynnika R obciążenia, wymagana jest korekta.
Program zawsze używa naprężenia wg Misesa do obliczenia naprężenia średniego. Ponieważ naprężenia wg Misesa są wartością dodatnią, program przypisuje im znak naprężenia głównego z największą algebraiczną wielkością w celu obliczenia skojarzonego naprężenia średniego.
Definicje
Przed przystąpieniem do dyskusji metod korekty, zdefiniujmy następujące zmienne dla cyklu naprężenia:
Smax = naprężenie maksymalne
Smin = naprężenie minimalne
ΔS = zakres naprężeń = Smaks. - Smin.
Sa = Naprężenie przemienne = (Smax - Smin)/2
Sśr. = naprężenie średnie = (Smax + Smin)/2
R = Współczynnik naprężenia = Smin./Smax
A = współczynnik amplitudy = Sa/Sśr.
Współczynniki naprężenia i amplitudy dla niektórych często spotykanych obciążeń podano niżej:
| Typ obciążenia
|
Współczynniki naprężenia i amplitudy
|
| Całkowicie odwrócony
|
R = -1, A = nieskończoność
|
| Zero - maksimum
|
R = 0, A = 1
|
| Zero - minimum
|
R = nieskończoność, A = -1
|
Metody korekty
W poniższych rozważaniach załóżmy:
Sca = skorygowane naprężenie przemienne (w oparciu o zerową średnią),
Sy = granica plastyczności,
Su = wytrzymałość graniczna
Oprogramowanie oferuje następujące metody obliczania S
ca:
| Metoda
|
Równanie
|
| 1. Metoda Goodmana - generalnie odpowiednia dla materiałów kruchych:
|
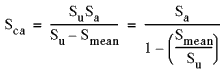
|
| 2. Metoda Gerbera - generalnie odpowiednia dla materiałów plastycznych
|
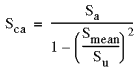
|
| 3. Metoda Soderberga - generalnie najbardziej konserwatywna
|
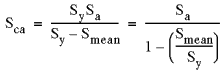
|
Zarówno dla przypadków o zmiennej, jak i stałej amplitudzie, dla każdego cyklu oprogramowanie oblicza naprężenie średnie oprócz naprężenia przemiennego, a następnie oszacowuje naprężenie skorygowane przy użyciu określonych kryteriów.