Fatigue damage assessment for components that operate in a random vibration environment is estimated in the frequency domain based on the statistical properties of the response stress power spectral density (PSD) function.
When structures or mechanical components are subjected to a random form of loading such as a wind turbine under wind load, an offshore structure under a wave load, or a car engine operating on different road surfacing profiles, fatigue life estimations are performed in the frequency domain.
The term vibration fatigue (or frequency-based fatigue) refers to the estimation of fatigue life where the loading and response (stress and strain histories) are random processes, and therefore are best described using statistical measures such as Power Spectral Density (PSD functions).
The statistical characteristics of the response
stress PSD can be obtained through the moments of the PSD function.
| Statistical Characteristics of PSD |
Equation |
| The nth spectral moment of the stress PSD
S(f) at frequency f (in units of Hz). |
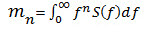 (Eq.1) (Eq.1)
|
| Root-mean-square value for a continuous stationary Gaussian process σ. |
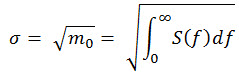 (Eq.2) (Eq.2)
|
| Average number of upward zero crossings E[0] for a typical 1 second sample. |
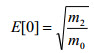 (Eq.3) (Eq.3)
|
| Average number of peaks E[p] for a typical 1 second sample. |
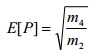 (Eq.4) (Eq.4)
|
| The irregularity factor γ varies between 0 and 1. It
approaches 1 as the stress signal approaches a narrow band process (for
a sine wave γ =1). It converges to 0.745 as the stress signal approaches
a white noise process. |
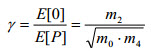 (Eq.5) (Eq.5)
or
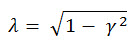 (Eq.6) (Eq.6)
|
The material fatigue properties are usually obtained from an S-N curve, which defines the
relationship between the stress range, S ( this is the stress variation from the maximum cyclic stress in tension to the minimum cyclic stress in compression) versus the mean cycles to failure, N.
For
most high cycle fatigue problems (N >= 104
), the S-N curve can be expressed in a simplified
form:
 (Eq.7)
(Eq.7)
where B and m are material properties varying with loading and environment conditions and are determined by fatigue testing experiments.
The accumulated damage E[AD] due to fatigue from random loading is based on the Palmgren-Miner's rule, and expressed as:
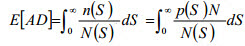 (Eq.8)
(Eq.8)
where n(S) is the number of cycles applied at stress range level S, p(S) is the probability
density function of the stress range. Substituting the equation of the simplified S-N curve in the equation above, a general equation
of fatigue damage from random stress response is obtained from:
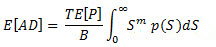 (Eq.9), where T is the time duration in sec of the random loading.
(Eq.9), where T is the time duration in sec of the random loading.
Three methods for fatigue damage estimate based on Eq.9 are available: Steinberg's three band method, Narrow band method, and Wirshing's method. Each method uses a different definition for the probability density function p(S).
Narrow Band method
In the narrow band method, the probability density function of peaks for a narrow band signal tends towards a Rayleigh distribution (Bendat J.S., Probability Functions for Random Responses. NASA report on Contact NASA-5-4590, 1964).
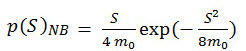 (Eq.10)
(Eq.10)
Substituting (Eq.10) in (Eq.9) and integrating results to the following expression for the fatigue damage estimate.
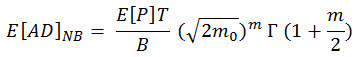 (Eq.11), where Γ(.) is the Gamma function.
(Eq.11), where Γ(.) is the Gamma function.
Wirsching's method
Wirsching’s method (Wirshing, P.H., Paez, T.L., and Ortiz K., Random Vibration, John Wiley & Sons Inc., New York, 1995) modifies the Narrow Band method with an empircal correction factor
to take into consideration a wide band process.
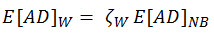 (Eq. 12)
(Eq. 12)
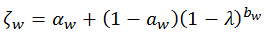 , (Eq. 13)
, (Eq. 13)
ζw is an empirical factor derived from Monte Carlo simulations that include a variety of spectral density functions.
αw and bw are best-fitting parameters given from:
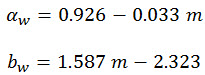 (Eq. 14)
(Eq. 14)
Steinberg's three band method
The assumption of the Steinberg’s method is that the probability density function of the random stress response follows a Gaussian distribution, and therefore the expected values of the stress response amplitudes are bound by certain probability levels:
- 68.27% chance that the amplitude of the stress cycles will not exceed the range of 2 times the root-mean-square of the stress response signal.
- 27.1 % chance that the amplitude of the stress cycles will not exceed the range of 4 times the root-mean-square of the stress response signal.
- 4.3% that the stress cycles will not exceed the range of 6 times the root-mean-square of the stress response signal.
There are no stress cycles occurring with ranges greater than 6 times the root-mean-square.
The expected fatigue damage is given by:
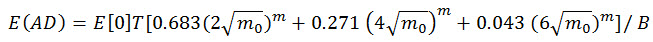 (Eq.15)
(Eq.15)
In Simulation, the stress PSD functions are the results from the dynamic - random vibration study that the fatigue study is based. The vonMises stress component is considered for the calculation of the expected damage due to fatigue for all three methods.