Processus aléatoire ou stochastique
De façon générale, un processus stochastique est considéré comme une famille de variables aléatoires ou un groupement d'un grand nombre d'enregistrements décrivant un phénomène physique. Les enregistrements peuvent être une fonction de temps {xk(t)} ou de fréquence {xk(f)}. Chaque enregistrement est quelque peu différent de tout autre enregistrement. Il est donc impossible d'inclure tous les enregistrements possibles dans l'analyse. A la place, un processus aléatoire est décrit en termes de propriétés statistiques. Chaque chargement d'une analyse de vibration aléatoire est un processus aléatoire. La réponse d'un modèle à ces chargements est également un processus aléatoire décrit en termes statistiques.
Fonction d'autocorrélation
La fonction d'autocorrélation d'un processus aléatoire décrit la corrélation entre les valeurs d'un enregistrements à différents moments. Elle est définie comme la valeur attendue du produit d'une variable aléatoire x(t) par une de ses versions à un autre moment.
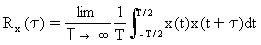 (Eq.1)
(Eq.1)
RMS (moyenne quadratique)
La valeur de la moyenne quadratique donne une mesure de l'énergie associée au processus aléatoire.
Elle est définie comme étant la valeur de la fonction d'autocorrélation pour τ = 0
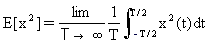 (Eq.2)
(Eq.2)
où E est appelé l'opérateur d'espérance. La racine carrée positive de la valeur moyenne est appelée la moyenne quadratique, ou RMS.
Ecart
La valeur de la moyenne quadratique d'un processus aléatoire par rapport à son μx moyen.
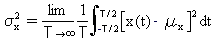 (Eq.3)
(Eq.3)
La racine carrée positive de l'écart est appelée l'écart standard.
Densité spectrale de puissance (PSD)
La densité spectrale de puissance est définie comme la transformée de Fourier de la fonction d'autocorrélation d'un processus aléatoire.
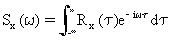 (Eq.4)
(Eq.4)
La densité spectrale de puissance décrit comment l'énergie du processus aléatoire est distribuée dans la représentation en fréquence.
Bruit blanc
Un signal de bruit blanc a une densité spectrale de puissance uniforme à toutes les fréquences. En d'autres termes, l'énergie du signal est distribuée uniformément dans toutes les fréquences.