Система уравнений движения линейной системы с n степенями свободы возбуждена изменяющейся во времени силой:
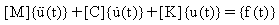 (Уравнение 1).
(Уравнение 1).
Используя преобразование координат, задайте систему n совместных уравнений, снижая до n независимых уравнений (каждое уравнение может быть решено независимо):
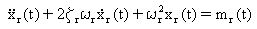 для r = 1, 2,...., n (Уравнение 2)
для r = 1, 2,...., n (Уравнение 2)
где xr(t) являются модальными координатами, связанными с узловыми координатами ur(t) посредством:
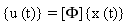 (Уравнение 3).
(Уравнение 3).
Вектор модальных нагрузок {m(t)} получается из:
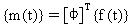 (Уравнение 4).
(Уравнение 4).
При условии, что возбуждения выражены функциями удельной мощностью спектра (PSD), решение может быть сформулировано в частотной области. Если матрица возбуждения PSD дана в виде [Sf(ω)], матрица модальный силы PSD определяется в виде:
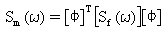 (Уравнение 5).
(Уравнение 5).
PSD модальной реакции перемещения [Sx(ω)] получено из:
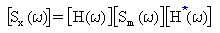 (Уравнение 6),
(Уравнение 6),
где [H(ω)] является модальной матрицей передаточных функций, а [H*(ω)] – ее комплексно-сопряженной матрицей. Для нормальных мод матрица передаточных функций является диагональной с диагональными элементами Hr(ω)
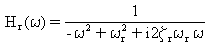 (Уравнение 7) и
(Уравнение 7) и
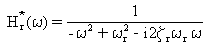 (Уравнение 8).
(Уравнение 8).
PSD реакции перемещения [Su(ω)] получается из (Уравнения 3).
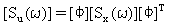 (Уравнение 9).
(Уравнение 9).
PSD реакций скорости и ускорения выражена посредством:
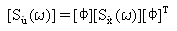 (Уравнение 10) и
(Уравнение 10) и
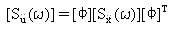 (Уравнение 11).
(Уравнение 11).
PSD модальной скорости и ускорения связана с PSD модального перемещения посредством:
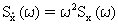 (Уравнение 12) и
(Уравнение 12) и  (Уравнение 13)
(Уравнение 13)
Уравнение 10 и Уравнение 11 могут быть перезаписаны в виде:
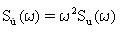 (Уравнение 14) и
(Уравнение 14) и 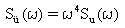 (Уравнение 15).
(Уравнение 15).
Модальные реакции автокорреляции с нулевой задержкой (т=0) в исчислении PSD модальной реакции вычислены из интегралов:
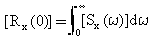 (Уравнение 16).
(Уравнение 16).
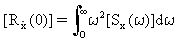 (Уравнение 17).
(Уравнение 17).
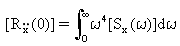 (Уравнение 18).
(Уравнение 18).
Из вышеприведенных уравнений, среднеквадратические реакции определены из диагональных элементов матрицы:
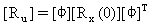 (Уравнение 19),
(Уравнение 19),
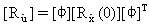 (Уравнение 20),
(Уравнение 20),
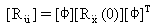 (Уравнение 21).
(Уравнение 21).
Среднеквадратическая реакция напряжения
Напряжения элемента {σ} определяются из узлового перемещения {u} при помощи:
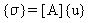 (Уравнение 22) или в единицах модального перемещения {x} посредством:
(Уравнение 22) или в единицах модального перемещения {x} посредством:
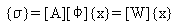 (Уравнение 23), где [Φ] является матрицей собственных векторов.
(Уравнение 23), где [Φ] является матрицей собственных векторов.
Матрица корреляции напряжения [Rσ] получается из:
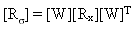 (Уравнение 24).
(Уравнение 24).