Utilice estudios armónicos para calcular la respuesta de estado estable pico ocasionada por cargas armónicas o excitaciones de la base.
Una carga armónica P se expresa como P = A sin (ωt + φ) donde: A es la amplitud, ω es la frecuencia, t es el tiempo y φ es el ángulo de fase. A continuación, se muestran cargas armónicas de ejemplo de frecuencias distintas w frente al tiempo:
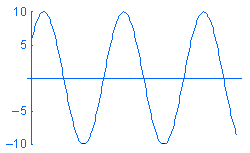
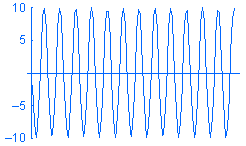
A pesar de que puede crear un estudio modal de historia-tiempo y definir cargas como funciones de tiempo, quizás no le interese en la variación transitoria de la respuesta con el tiempo. En esos casos, puede ahorrar tiempo y recursos solucionando la respuesta de estado estable pico en el intervalo de frecuencia operacional deseado mediante análisis armónico.
Por ejemplo, un motor montado en una mesa de pruebas transfiere cargas armónicas al sistema de soporte a través de los pernos. Puede modelar el sistema de soporte y definir un estudio armónico para evaluar los desplazamientos de estado estable pico, tensiones, etc. para las frecuencias en funcionamiento del motor. Puede aproximar el motor mediante una masa distribuida.
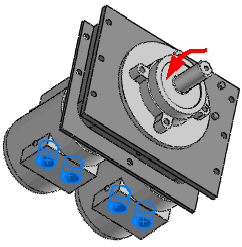
Después de ejecutar el estudio, puede ver amplitudes pico de los parámetros de respuesta (tensiones, desplazamientos, aceleraciones y velocidades), así como gráficos de respuesta de los ángulos de fase de los parámetros de respuesta del rango de frecuencias en funcionamiento.
Al ejecutar un estudio armónico, el trazado de contorno de un parámetro de respuesta muestra los valores pico absolutos del historial de tiempo sinusoidal de respuesta en un determinado paso de frecuencia. La pieza sinusoidal transitoria del parámetro de respuesta y su ángulo de fase no se muestran en el trazado. Para un paso de frecuencia de funcionamiento próximo al de la frecuencia natural del modelo, el trazado de forma modal es una representación más realista de la geometría deformada que el trazado de contorno de desplazamiento en una determinada frecuencia.
Puede crear un gráfico de respuesta del ángulo de fase para un parámetro de respuesta (desplazamiento, tensión, velocidad o aceleración) en todos los pasos de frecuencia de la solución.
Las opciones de amortiguamiento modal, de Rayleigh y compuesta están disponibles para este tipo de análisis.