Büyük gerinim plastisitesi teorisinde, bir logaritmik gerinim ölçümü şu şekilde tanımlanır: 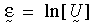
Burada U, deformasyon gradyanı F'nin (F = R U; R rotasyon tensörüdür) sağ taraf polar ayrışımından elde edilen sağ uzama tensörüdür. Artımlı logaritmik gerinim şu şekilde tahmin edilir: 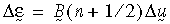
Burada B(n+1/2), çözüm adımı n+1/2'de tahmin edilen gerinim-yer değiştirme matrisidir ve Δu, artımlı yer değiştirme vektörüdür. Yukarıdaki formülün, tam formülün ikinci dereceden yaklaşık ifadesi olduğu unutulmamalıdır.
Bünye modelini doğru bir şekilde çerçeve sabiti veya objektifi yapmak için gerilim oranı Green-Naghdi oranı olarak alınır. Gerilim oranı global sistemden R sistemine dönüştürülür:
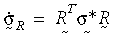
Tüm bünye modeli, küçük gerinim teorisine şekil açısından benzer olacaktır. Büyük gerinim plastisitesi teorisi von Mises akma kriterine, ilişkili akış kuralına ve izotropik veya kinematik sertleştirmeye (iki doğrusal veya çok doğrusal) uygulanır. Malzeme özelliğinin sıcaklığa bağımlılığı, iki doğrusal sertleştirme tarafından desteklenir. Geçerli örnekte radyal geri dönüş algoritması kullanılmaktadır. Buradaki temel fikir, dik vektör N'nin şu formülasyonla yakınsanmasıdır:
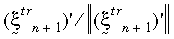
burada 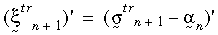
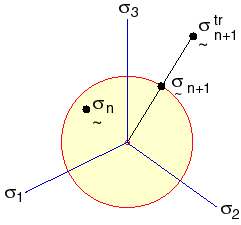
Aşağıdaki şekilde, yukarıdaki iki denklem gösterilmektedir.
Eleman kuvveti vektörü ve katılık matrisleri, güncellenen Lagrangian formülasyonuna dayalı olarak hesaplanır. Cauchy gerilimleri, logaritmik gerinimler ve geçerli kalınlık (sadece kabuk elemanları) çıktı dosyasına kaydedilir.
Geçerli örnekteki elastisite, küçük elastik gerinimler olduğunu varsayan fakat rastgele büyük plastik gerinimlere izin veren bir hiperelastik formda modellenmiştir. Büyük gerinim elastisite problemleri (lastik benzeri) için Mooney-Rivlin gibi hiperelastik malzeme modellerini kullanabilirsiniz.
Çok doğrusal gerilim-gerinim eğrisini tanımlamada Cauchy (gerçek) gerilimi ve logaritmik gerinim kullanılmalıdır.