The following integration methods are used for random vibration studies.
Standard Method
The standard method for random vibration analysis proceeds as follows:
- Certain frequency points are selected around each requested natural mode. Locations of these points depend on the value of the biasing parameter p.
For a biasing parameter of 1.0, all the frequency points are uniformly distributed between the natural frequencies. If the biasing parameter is greater than 1.0, the points are selected closer to the natural frequencies. The default values for the frequency points and the biasing parameter are given as a function of the first mode's damping ratio ζ. For an illustration on the selection of the frequency points click here.
Default values for the frequency points and the biasing parameter as a function of ζ are given below:
| Modal Damping Ratio
|
Number of Frequencies (Default)
|
Biasing Parameter (Default)
|
|---|
| ζ < 0.01
|
21 |
11
|
| 0.01 < ζ < 0.1
|
21-4.34 ln(ζ /0.01)
|
11-3.47 ln(ζ /0.01)
|
| ζ > 0.1
|
11
|
3
|
The software applies the default values given in Table 1 when zero (0) is defined for both the Number of frequency points and Biasing Parameter.
- Modal psds of response are evaluated at each of the frequency points. The cross-mode cut-off ratio (RATIO) sets a limit on the ratio of all possible pairs of natural frequencies (wi / wj, i > j).
This means that for each pair of modes with wi / wj > RATIO, the cross-spectral density terms are neglected. Cross-mode effects are not considered for RATIO =1.
- The modal psds are then numerically integrated over the specified frequency range to yield the mean squared values and covariances of the modal response. The integration is carried out numerically using Gauss integration of order 2 or 3 over each frequency interval, based on a log-log interpolation. The mean squared response is obtained by summing the interval contributions.
- Finally, transformation from modal to nodal yields the rms displacements, velocities, and accelerations of the system.
Approximate Method
The standard method of integration can be computationally time consuming due to the numerical integration of large matrices. The approximate method of integration performs a simplified solution by making the following assumptions:
- Neglecting the cross-mode response, Sx(ω) , that is the effect of one mode on another, i.e.
 (Equation 1)
(Equation 1)
- The psd of excitations are considered constant around each mode. Thus, each mode is assumed to be excited by "white noise" with spectral density Sn, where;
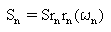 (Equation 2)
(Equation 2)
ωn is the natural frequency of mode n (n = 1,2,...nf).
For white noise, the mean square responses can be determined analytically for the modal responses:
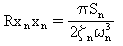 (Equation 3)
(Equation 3)
 (Equation 4)
(Equation 4)
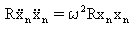 (Equation 5).
(Equation 5).