Description
A plane strain rubber cylinder of diameter 0.4m is pressed between two frictionless plates. Determine the force-deflection curve for the cylinder and the distribution of the von Mises stresses when the applied displacement equals one-half of the initial diameter of the cylinder.
File Name
Browse to drive
letter:\Users\Public\Public Documents\SOLIDWORKS\SOLIDWORKS
version\samples\Simulation
Examples\Verification\Nonlinear_Static_17.SLDASM and open the
file.
Study Type
Nonlinear.static
Meshing Parameters
Use a Global size of 1.0 ".
Material Model
Hyperelastic material with Mooney-Rivlin type model.
Material Properties
Cylinder: Poisson's ratio in XY dir = 0.4999, First material constant = 0.293 MPa, Second material constant = 0.177 MPa, Mass density = 1100 kg/m3.
Plate: Elastic modulus = 1000 GPa, Mass density = 7800 kg/m3
Modeling Hints
Due to symmetry, only a quarter of the model is considered.
Restraints and Loads
A displacement of 0.1 m (one-half of the prescribed displacement at the top plate) is applied on the top face of the quarter cylinder. Plane-strain conditions are modeled by prescribing zero UZ displacement on all faces in the XY plane. The contacting face of the plate is not allowed to move along the Y direction to simulate a rigid body.
Results
The von-Mises stress distribution for the cylinder is shown below. The unit is MPa.
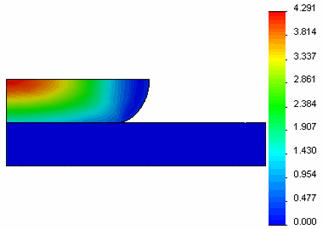
The force-deflection curve for the cylinder agrees with the finite element solution provided by the reference.
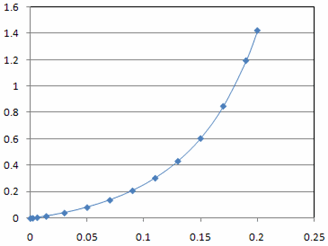
The X-axis shows UY displacement of cylinder's top face in m. The Y-axis shows contact force for unit width in MN/m. between the cylinder and plate.
The results of the nonlinear analysis have been processed by a graphing software to generate the above graph. The displacements are multiplied by 2 to account for symmetry. The contact force is reported on the contacting face of the cylinder. It is then divided by width 0.02 m (z direction) and multiplied by 2 (due to symmetry).
Reference
T. Sussman and K. J. Bathe, "A Finite Element Formulation for Nonlinear Incompressible Elastic and Inelastic Analysis," Computers and Structures, Vol. 26. No. 1/2, pp. 357-409, 1987.