Description
Determine the first three natural frequencies of a beam with length 120", and cross section: ISO square tube of size: 20 x 20 x 2 for various support conditions.
File Name
Browse to
drive letter:\Users\Public\Public
Documents\SOLIDWORKS\SOLIDWORKS
version\samples\Simulation
Examples\Verification\Frequency_17.SLDPRT and open the
file.
Material Properties
Alloy Steel. Modulus of elasticity = 30,457,924 psi, Poisson's ratio = 0.28, Mass density = (0.27818 lb/in3) / (386.4 in /sec2).
Beam Properties
ISO square tube of size: 20 x 20 x 2. Cross sectional area: 0.2072 in2; Moments of Inertia: Ix = 0.0166 in4, Iy = 0.0166 in4.
Beam Restraints
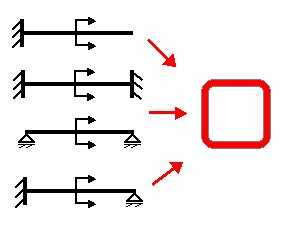
Four cases are considered for the end restraints:
- Pinned - Pinned
- Fixed - Free
- Fixed - Fixed
- Fixed - Pinned
Results
| |
|
Theory |
SOLIDWORKS Simulation |
| Frequencies (Hz)
|
|
|
| (a) Pinned - Pinned |
1st
and 2nd Mode |
6.351 |
6.353 |
| 3rd
and 4th |
25.403 |
25.409 |
| 5th
and 6th |
57.156 |
57.134 |
| (b) Fixed - Free |
1st
and 2nd Mode |
2.262 |
2.253 |
| 3rd
and 4th |
14.178 |
13.962 |
| 5th
and 6th |
39.7 |
38.699 |
| (c) Fixed - Fixed |
1st
and 2nd Mode |
14.396 |
14.401 |
| 3rd
and 4th |
39.684 |
39.683 |
| 5th
and 6th |
77.797 |
77.685 |
| (d) Fixed - Pinned |
1st
and 2nd Mode |
9.921 |
9.925 |
| 3rd and 4th
|
32.150 |
32.155 |
| 5th and 6th
|
67.079 |
67.025 |
Natural frequencies (Hz): fi = (λi2 / 2 π L2)*( E I / m )1/2 (for i =1, 2, 3, ...)
where:
- E: Modulus of elasticity
- I: Area moment of inertia of beam (neutral axis)
- L: Span of beam
- M: Mass per unit length of beam
| |
i |
λi
|
| (a) Pinned - Pinned |
1 |
π |
| 2 |
2*π |
| 3 |
3*π |
| (b) Fixed - Free |
1 |
1.875104 |
| 2 |
4.694091 |
| 3 |
7.854757 |
| (c) Fixed - Fixed |
1 |
4.730041 |
| 2 |
7.853205 |
| 3 |
10.995608 |
| (d) Fixed - Pinned |
1 |
3.926602 |
| 2 |
7.068582 |
| 3 |
10.210176 |
Reference
Robert D. Blevins, "Formulas for Natural Frequency and Mode Shape", Krieger Publishing Company, Florida, Reprint Edition 2001, pp. 108-109.