Determine the hoop stress distribution along the thin edge of an
eccentric tube subjected to constant internal pressure and a cyclic temperature gradient varying
linearly through thickness.
All
dimensions are in mm.
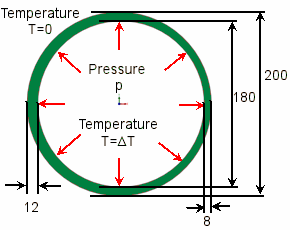
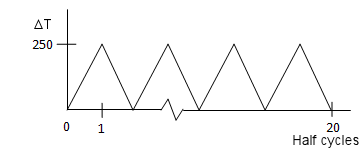
Here, p = 6.7413 MPa and ΔT is applied as
shown:
|
File Name
|
Open drive
letter:\Users\Public\Public Documents\SOLIDWORKS\SOLIDWORKS version\samples\Simulation
Examples\Verification\NAFEMS_NL9.SLDPRT.
|
|
Study Type
|
Nonlinear static with large strain and large displacement
formulations
|
|
Mesh Size
|
Use a standard mesh with a global element size of 2 mm.
|
|
Material Properties
|
| Material Property |
Value |
| Model Type: Plasticity - von Mises |
| Elasticity modulus (E) |
160000 N/m2 |
| Poisson's ratio (ν) |
0.3 |
| Yield stress (σy) |
160 N/m2 |
| Coefficient of thermal expansion
(α) |
2 x 10-5
/K |
|
|
Modeling Hints
|
Owing to symmetry, consider only half of the model.
|
Results
First, run the Thermal Study. A linear
distribution of temperature gradient is obtained through the thickness. Then, run the
Nonlinear Study. Plot the result for hoop stress
(SY - reference Axis 1) along the thinner
edge (8 mm thick) from the Nonlinear Study.
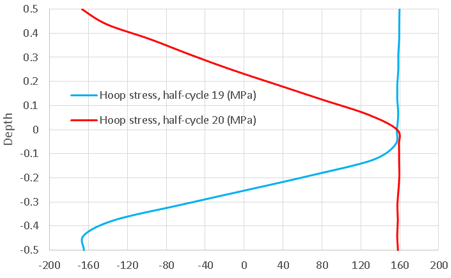
The blue
line shows the hoop stresses at
half cycle 19 (MPa). The
red line shows the hoop stresses at half cycle 20 (MPa). The X-axis is the parametric
thickness measured from the middle
section.
The through thickness stress variation curves agree with the finite element
solution provided in the reference.
Reference
NAFEMS Publication R0026, The International Association for the Engineering
Analysis Community, “Selected Benchmarks for Material nonlinearity,
1993”.