Das Werkzeug Unterbestimmte Körper erkennt alle starren (oder freien) Körpermodi, die nicht ausreichend durch Haltevorrichtungen, Verbindungsstücke oder Interaktionsbedingungen abgestützt werden.
Um unterbestimmte Körper zu erkennen, führen Sie einen der folgenden Schritte aus:
- Klicken Sie in einer statischen Studienstruktur mit der rechten Maustaste auf Verbindungen
 und dann auf Unterbestimmte Körper
und dann auf Unterbestimmte Körper  .
.
- Wählen Sie im CommandManager die Option Diagnosewerkzeuge und klicken Sie auf Unterbestimmte Körper
 .
.
- Wählen Sie im Dialogfeld die Option Unterbestimmte Körper automatisch erkennen aus.
Bevor Sie das Werkzeug Unterbestimmte Körper ausführen, sollten Sie realistische Materialien, Lasten und Randbedingungen für Ihr Modell definieren. Die Eigenschaften der Studie sollten die Betriebsbelastung und die Randbedingungen des Modells, das Sie versuchen zu analysieren, so genau wie möglich reflektieren.
Der Algorithmus prüft, ob für jedes Teil einer Baugruppe freie Verschiebungen und Rotationen in der globalen X-, Y- und Z-Richtung und auch in schräge Richtung möglich sind. Er kann auch Instabilitätsprobleme in Baugruppen mit Ketten- (oder Scharnier-) Mechanismen zwischen den Teilen erkennen. In Fällen, in denen freie Körpermodi erkannt werden, werden diese mit dem Werkzeug Unterbestimmte Körper entsprechend animiert.
Die Erkennung von unterbestimmten Körpern basiert auf der Transformation der Steifigkeitsmatrix, die mit einem Finite-Elemente-Modell verbunden ist, in eine reduzierte Steifigkeitsmatrix (normalerweise mit drei Translations- und drei Rotationsfreiheitsgraden pro Körper). Die unterbestimmten Modi des reduzierten Systems entsprechen dem ursprünglichen Gleichungssystem.
Die Umwandlung der globalen Steifigkeitsmatrix in eine verkleinerte Steifigkeitsmatrix wird abgeschlossen durch:
- Einführung eines einzigen repräsentativen Knotens (Referenzpunkt) mit sechs Freiheitsgraden für jeden Körper, die die Translations- und Rotationsbewegung des jeweiligen Körpers darstellen
- Umwandlung der Steifigkeitsmatrizen der Elemente durch Ersetzen der ursprünglichen Freiheitsgrade durch die Freiheitsgrade der repräsentativen Knoten
- Zusammensetzen der umgewandelten Elementsteifigkeitsmatrizen zur Bestimmung der verkleinerten Steifigkeitsmatrix
Vorteile
Die Lösung ist viel schneller. Die Leistungsverbesserung beruht auf der Anwendung des Verfahrens der Singulärwertzerlegung (SVD), das für die reduzierte Steifigkeitsmatrix durchgeführt wird. Die reduzierten Steifigkeiten werden aus der Grenzflächenwechselwirkung zwischen Körpern berechnet, die aus Randbedingungen, Verbund- und Kontaktinteraktionen oder Verbindungselementen resultieren.
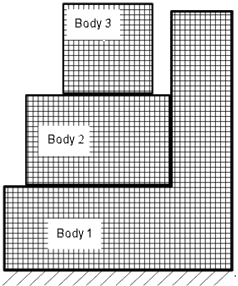
Im Folgenden finden Sie ein Beispiel für eine reduzierte Steifigkeitsmatrix:
|
|
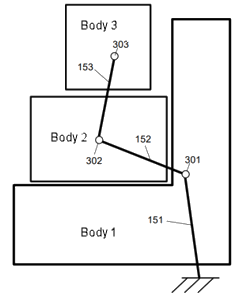 |
| Jeder Körper reduziert sich auf einen Referenzpunkt in der Steifigkeitsmatrix. Die globale Steifigkeitsmatrix reduziert sich von hunderttausenden von Freiheitsgraden auf nur 18 (3 Körper x 6 Freiheitsgrade). |
Die Methode berücksichtigt Steifigkeiten, die aus den Wechselwirkungen zwischen den Körpern resultieren. Die Körper 1 und 2 berühren sich, sodass die Methode die Wirkung ihrer Steifigkeiten zwischen ihren Bezugspunkten berücksichtigt. Die Methode berücksichtigt auch Steifigkeiten, die von Randbedingungen stammen, zum Beispiel die Steifigkeit zwischen Körper 1 und dem Boden. |
Mit der SVD-Technik wird die reduzierte Steifigkeitsmatrix in drei Matrizen zerlegt.
Die Vektoren U und V sind orthonormal zueinander und beschreiben die Form des Verschiebungsfeldes. Die mittlere Matrix ist eine Diagonalmatrix. Die diagonalen Terme stellen die relativen Steifigkeiten der Verbindungen zwischen den Körpern oder zwischen einem Körper und dem Boden dar. Wenn einer der diagonalen Ausdrücke Null oder fast Null ist, ist dies ein Hinweis auf einen Modus für starre Körper.
Sie können Animationen der unterbestimmten Verschiebungen der gesamten Baugruppe anzeigen.
Sie können animierte Verschiebungen oder Rotationen in Schrägrichtungen anzeigen.