Die Bewertung der Ermüdungsschäden von Komponenten, die in einer Umgebung mit zufälliger Vibration betrieben werden, wird in der Frequenzdomäne basierend auf den statistischen Eigenschaften der Funktion Spektrale Belastungs-Leistungsdichtenreaktion (PSD) geschätzt.
Wenn Strukturen oder mechanische Komponenten zufälligen Belastungen ausgesetzt werden, wie z. B. eine Windenergieanlage unter Windlast, eine Offshore-Struktur unter Wellenlast oder ein Automotor auf unterschiedlichen Straßenbelagprofilen, erfolgt die Schätzung der Lebensdauer in der Frequenzdomäne.
Der Begriff Vibrationsermüdung (oder frequenzbasierte Ermüdung) bezieht sich auf die Schätzung der Ermüdungslebensdauer, wenn die Belastung und Reaktion (Spannungs- und Dehnungsverläufe) zufällige Prozesse sind und daher am besten mit statistischen Messgrößen wie der spektralen Leistungsdichte (PSD-Funktionen) ausgedrückt werden.
Die statistischen Merkmale der Reaktions-Spannungs-PSD können über die Momente der PSD-Funktion abgerufen werden.
| Statistische Merkmale von PSD |
Gleichung |
| Das n-te spektrale Moment der Spannungs-PSD S(f) bei Frequenz f (in Hz). |
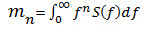 (Gl. 1) (Gl. 1)
|
| Quadratischer Mittelwert für einen kontinuierlichen stationären Gaußschen Prozess σ. |
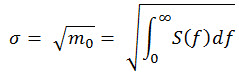 (Gl. 2) (Gl. 2)
|
| Durchschnittliche Anzahl der Nulldurchgänge nach oben E[0] für eine typische Stichprobe von 1 Sekunde. |
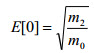 (Gl. 3) (Gl. 3)
|
| Durchschnittliche Anzahl der Maxima E[p] für eine typische Stichprobe von 1 Sekunde. |
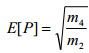 (Gl. 4) (Gl. 4)
|
| Der Unregelmäßigkeitsfaktor γ variiert zwischen 0 und 1. Er nähert sich 1, wenn das Spannungssignal sich einem Schmalbandprozess nähert (für eine Sinuswelle γ = 1). Er konvergiert zu 0,745, wenn das Spannungssignal sich einem Rauschprozess nähert. |
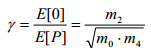 (Gl. 5) (Gl. 5)
oder
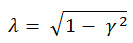 (Gl. 6) (Gl. 6)
|
Die Materialermüdungseigenschaften werden in der Regel aus einer S-N-Kurve abgelesen, die die Beziehung zwischen dem Spannungsbereich S (dies ist die Spannungsvariation aus der maximalen zyklischer Spannung im Spannungsverhältnis zur minimalen zyklischen Spannung bei Kompression) und dem Mittelwert der Zyklen bis zum Versagen N definiert.
Bei den meisten Problemen durch hohe Ermüdung (N >= 104) kann die S-N-Kurve in vereinfachter Form ausgedrückt werden:
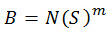 (Gl. 7)
(Gl. 7)
wobei B und m Materialeigenschaften sind, die mit den Last- und Umgebungsbedingungen variieren und in Ermüdungsexperimenten bestimmt werden.
Den angesammelten Schaden E[AD] aufgrund von Ermüdung durch zufällige Last basiert auf der Palmgren-Miner-Regel und wird wie folgt ausgedrückt:
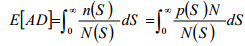 (Gl. 8)
(Gl. 8)
wobei n(S) die Anzahl der im Spannungsbereich S angewendeten Zyklen und p(S) die Wahrscheinlichkeitsdichtefunktion des Spannungsbereichs ist. Durch die Ersetzung der Gleichung der vereinfachten S-N-Kurve in der obigen Gleichung wird eine allgemeine Gleichung für Ermüdungsschäden zufällige Spannungsreaktionen erreicht:
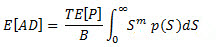 (Gl. 9), wobei T die Zeitdauer in Sek. der zufälligen Belastung ist.
(Gl. 9), wobei T die Zeitdauer in Sek. der zufälligen Belastung ist.
Basierend auf Gl. 9 sind drei Methoden zur Schätzung des Ermüdungsschadens verfügbar: Die Dreibandmethode von Steinberg, die Schmalbandmethode und Wirshings Methode. Jede Methode verwendet eine andere Definition für die Wahrscheinlichkeitsdichtefunktion p(S).
Schmalbandmethode
Bei der Schmalbandmethode tendiert die Wahrscheinlichkeitsdichtefunktion der Maxima für ein Schmalbandsignal zu einer Rayleigh-Verteilung (Bendat J.S., Probability Functions for Random Responses. NASA report on Contact NASA-5-4590, 1964).
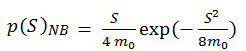 (Gl. 10)
(Gl. 10)
(Gl. 10) wird in (Gl. 9) ersetzt und die Ergebnisse werden in den folgenden Ausdruck für die Ermüdungsschadenschätzung integriert.
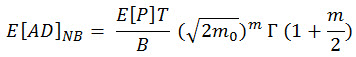 (Gl. 11), wobei Γ(.) die Gamma-Funktion ist.
(Gl. 11), wobei Γ(.) die Gamma-Funktion ist.
Wirsching-Methode
Die Wirsching-Methode (Wirshing, P.H., Paez, T.L. und Ortiz K., Random Vibration, John Wiley & Sons Inc., New York, 1995) modifiziert die Schmalbandmethode mit einem empirischen Korrekturfaktor zur Berücksichtigung eines Breitbandprozesses.
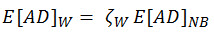 (Gl. 12)
(Gl. 12)
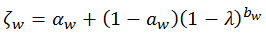 , (Gl. 13)
, (Gl. 13)
ζw ist ein empirischer Faktor, der von Monte-Carlo-Simulationen abgeleitet wurde, die eine Vielzahl von spektralen Leistungsdichtefunktionen umfassen.
αw und bw sind die am besten geeigneten Parameter aus:
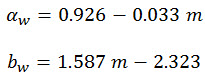 (Gl. 14)
(Gl. 14)
Dreibandmethode von Steinberg
Die Steinberg-Methode nimmt an, dass die Wahrscheinlichkeitsdichtefunktion der zufälligen Spannungsreaktion einer Gauß-Verteilung folgt und die erwarteten Werte der Spannungsreaktionsamplituden daher an bestimmte Wahrscheinlichkeitsstufen gebunden sind:
- 68,27 % Chance, dass die Amplitude der Spannungszyklen den Bereich des doppelten quadratischen Mittelwerts des Spannungsreaktionssignals nicht übersteigt.
- 27,1 % Chance, dass die Amplitude der Spannungszyklen den Bereich des vierfachen quadratischen Mittelwerts des Spannungsreaktionssignals nicht übersteigt.
- 4,3 % Chance, dass die Amplitude der Spannungszyklen den Bereich des sechsfachen quadratischen Mittelwerts des Spannungsreaktionssignals nicht übersteigt.
Es gibt keine Spannungszyklen mit Bereichen, die größer als das Sechsfache des quadratischen Mittelwerts sind.
Der erwartete Ermüdungsschaden ist gegeben durch:
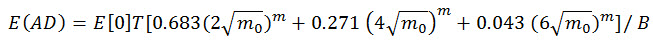 (Gl. 15)
(Gl. 15)
In Simulation sind die Spannungs-PSD-Funktionen das Ergebnis der dynamisch-zufälligen Vibrationsstudie, auf der die Ermüdungsstudie basiert. Die Von-Mises-Spannungskomponente wird bei der Berechnung der erwarteten Schäden aufgrund von Ermüdung für alle drei Methoden berücksichtigt.