Como o nitinol geralmente é usado pela sua capacidade de suportar deformações finitas, para este modelo é empregada a teoria de grandes deformações usando deformações logarítmicas com a fórmula de Lagrange atualizada.
O modelo constitutivo é, portanto, construído para relacionar as deformações logarítmicas e os componentes de tensão de Kirchhoff. Entretanto, no fim do processo, a matriz constitutiva e o vetor de tensão serão transformados para apresentar as tensões (verdadeiras) de Cauchy.
|
σs
t1, σf
t1
|
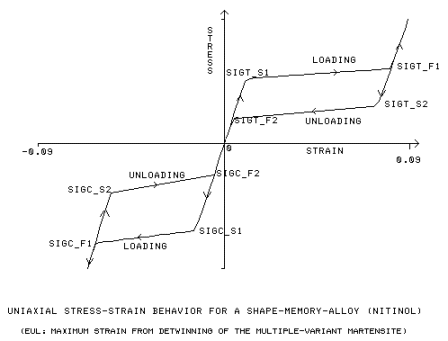
Tensões de campo inicial e final para carregamento de tensão [SIGT_S1, SIGT_F1]
|
|
σs
t1, σf
t1
|
Tensões de campo inicial e final para carregamento de tensão [SIGT_S1, SIGT_F1]
|
|
σs
t1, σf
t1
|
Tensões de campo inicial e final para carregamento de tensão [SIGT_S1, SIGT_F1]
|
|
σs
t1, σf
t1
|
Tensões de campo inicial e final para carregamento de tensão [SIGT_S1, SIGT_F1]
|
|
eul
|
(Deformação plástica de tensão máxima) *(3/2)0.5
|
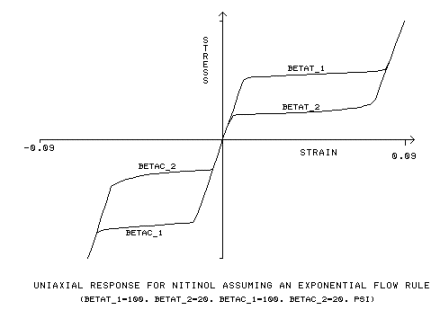
A regra do fluxo exponencial utiliza constantes de entrada adicionais, β
t1, β
t2, β
c1, β
c2:
|
βt1
|
bt1 = parâmetro de material, medição da velocidade de transformação para a carga de tração, [BETAT_1]
|
|
βt2
|
bt2 = parâmetro de material, medição da velocidade de transformação para o descarregamento de tensão, [BETAT_2]
|
|
βc1
|
bc1 = parâmetro de material, medição da velocidade de transformação para o carregamento de compressão, [BETAC_1]
|
|
βc2
|
bc2 = parâmetro de material, medição da velocidade de transformação para o descarregamento de compressão, [BETAC_2]
|
Critério de resistência
Para modelar a possibilidade da dependência da pressão da transformação de fase, é utilizada uma função de carregamento do tipo Drucker-Prager para o critério de resistência:
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RI
f = 0
onde
σ(bar) = tensão efetiva
p = tensão média (ou pressão hidrostática)
α = sqrt(2/3) (σsc1 - σst1 ) / (σsc1 + σst1)
Rf
I = [ σf
I(sqrt(2/3) + α)], I = 1 para carregamento e 2 para descarregamento