La función Blatz-Ko de densidad de energía correspondiente a la deformación unitaria resulta útil para modelar gomas o cauchos, como la espuma de poliuretano compresible, y puede expresarse de la siguiente manera:
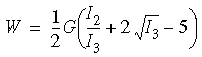
donde:
- G = E / 2(1+ν) es el módulo cortante sujeto a deformaciones infinitesimales, E es el módulo de elasticidad de Young, ν es el coeficiente de Poisson
- Ik (k=1,..3) son las constantes del tensor de deformación de Cauchy-Green C=Ik ©)
- C = 2ε +I, ε es el tensor de deformación unitaria lagrangiano e I es la matriz de identidad.
La expresión anterior contiene únicamente una constante de material G. Puesto que v = 0,25 para el modelo de Blatz-Ko, la única propiedad de material que se considera es el módulo de Young.
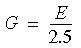
El modelo de Blatz-Ko actualmente sólo es admitido por elementos sólidos (calidad alta y de borrador).
El modelo de Blatz-Ko seleccionado es una forma simplificada de la expresión obtenida por Blatz y Ko (1962) para modelar la deformación de una goma de espuma de poliuretano altamente compresible. La aproximación a la energía de deformación unitaria se realizó mediante la siguiente expresión:
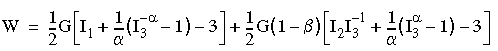
donde
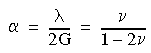
Posteriormente, se propuso una forma específica de esta familia de tres parámetros de potencial elástico en la que se asumieron los siguientes valores de las constantes α, β y ν: α = 0,5, β = 0 y ν = 0,25.