由于镍钛诺通常因其能承受有限应变而被使用,因此对于此模型可使用借助对数应变的大型应变理论以及更新的拉格朗日公式。
这样,可以建立本构模型,使对数应变与基尔霍夫应力分量相联系。但是,本构矩阵和应力向量最后都会进行变换以表示 Cauchy(真实)应力。
|
σs
t1、σf
t1
|
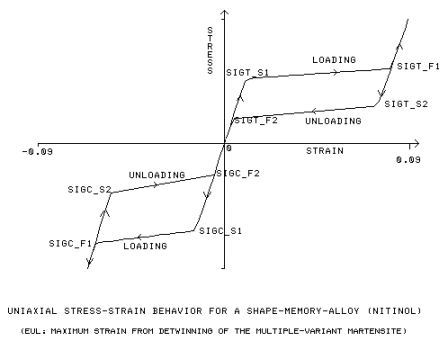
张力装载 [SIGT_S1, SIGT_F1] 的初始屈服应力和最终屈服应力
|
|
σs
t2、σf
t2
|
张力卸载 [SIGT_S2, SIGT_F2] 的初始屈服应力和最终屈服应力
|
|
σs
c1、σf
c1
|
压缩装载 [SIGC_S1, SIGC_F1] 的初始屈服应力和最终屈服应力
|
|
σs
c2、σf
c2
|
压缩卸载 [SIGC_S2, SIGC_F2] 的初始屈服应力和最终屈服应力
|
|
eul
|
(最大张力塑料应变)*(3/2)0.5
|
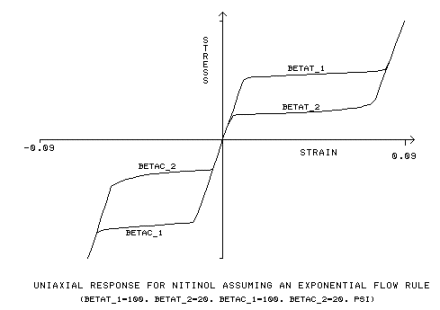
指数流动规则使用附加的输入恒定值 β
t1、β
t2、β
c1、β
c2:
|
βt1
|
材料参数,测量张力装载的转换速度 [BETAT_1]
|
|
βt2
|
材料参数,测量张力卸载的转换速度,[BETAT_2]
|
|
βc1
|
材料参数,测量压缩装载的转换速度,[BETAC_1]
|
|
βc2
|
材料参数,测量压缩卸载的转换速度,[BETAC_2]
|
屈服准则
为了建立相位变换的压力依赖的可能性模型,在屈服准则中使用 Drucker-Prager 类型的装载函数:
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RI
f = 0
其中
σ(bar) = 有效应力
p = 平均应力(或流体静压)
α = sqrt(2/3) (σsc1 - σst1 ) / (σsc1 + σst1)
Rf
I = [ σf
I(sqrt(2/3) + α)],I = 1 代表装载,而 2 代表卸载