La fonction de densité d'énergie de déformation de Mooney-Rivlin est exprimée ainsi :
| Constantes du matériau Mooney-Rivlin |
Equation de densité d'énergie |
| Formulation à deux constantes |
 |
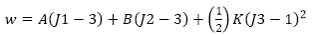| Formulation à cinq constantes |
 |
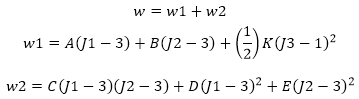| Formulation à six constantes |
 |
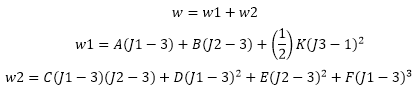- JI, J2 et J3 sont les invariants réduits du tenseur de déformation Cauchy-Green, et peuvent être exprimés en fonction du rapport d'allongement principal
- A, B, C, D, E et F correspondent à la première, la deuxième, la troisième, la quatrième, la cinquième et la sixième constante de matériau du modèle de matériau Mooney-Rivlin. Vous entrez ces constantes dans la boîte de dialogue Propriétés du matériau.
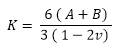, = Coefficient de Poisson
On a observé qu'au fur et à mesure qu'un matériau approche l'incompressibilité, le troisième invariant, III, s'approche de l'unité alors que K s'approche de l'infini. Par conséquent, pour les valeurs de coefficient de Poisson proches de 0,5, le dernier terme dans W1 reste solidaire et une solution peut être obtenue.
Le modèle de matériau de Mooney-Rivlin peut être utilisé avec des éléments volumiques et des coques épaisses.
Les constantes de Mooney-Rivlin sont automatiquement calculées lorsque l'option Utiliser les données de la courbe pour calculer les constantes du matériau est sélectionnée dans la boîte de dialogue Matériau. Les constantes sont enregistrées dans un fichier texte avec l'extension .log dans le dossier de résultats de l'étude active.