Les matériaux élastiques qui ont la capacité de dissiper de l'énergie mécanique à cause d'effets visqueux sont qualifiés de matériaux viscoélastiques.
Pour l'état de contraintes multi-axiales, la relation constitutive peut être exprimée ainsi :
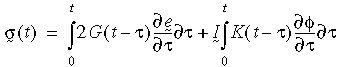
où: e(bar) et φ sont les déformations déviatorique et volumétrique ; G(t - τ) et K(t - τ) représentent les fonctions de relaxation de cisaillement et d'élasticité volumique.
Les fonctions de relaxation peuvent être représentées par le modèle mécanique généralement appelé modèle Maxwell généralisé et ayant les expressions suivantes :
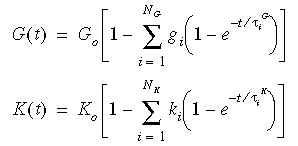
où: G0 = E / 2(1+ ν), module de cisaillement initial (t=0)
et K0= E / 3(1 -2ν), module d'élasticité volumique initial (t=0)
gi, ki, τi
G et τi
K sont les i-ème modules de cisaillement et d'élasticité volumique et leurs temps correspondants.
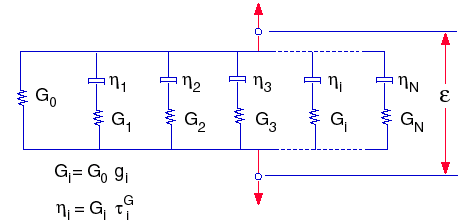
L'effet de la température sur le comportement du matériau est basé sur le principe de correspondance temps-température. L'expression mathématique du principe est la suivante :
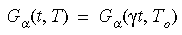
où γt représente le temps réduit et γ la fonction de décalage. L'équation de WLF (Williams-Landel-Ferry) permet d'approcher la fonction :
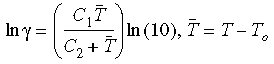
où T0 représente la température de référence généralement choisie comme température de transition de Glass ; C1 et C2 sont des constantes dépendant du matériau.
| Paramètre |
Propriétés du matériau |
|---|
| Paramètres linéaires élastiques |
Module d'élasticité suivant X
|
|
Coefficient de Poisson suivant XY
|
|
Module de cisaillement suivant XY
|
| Paramètres de fonctions de relaxation |
Module de relaxation en cisaillement (1 à 8) (représentent g1, g2, ...,g8 dans les équations du modèle de Maxwell généralisé)
|
|
Constantes de temps (Module de relaxation de cisaillement 1 à 8) (représentent τ1
g, τ2
g,..., τ8
g dans les équations du modèle de Maxwell généralisé) |
|
Module de relaxation de compressibilité (1 à 8) |
|
Constantes de temps (Module de relaxation d'élasticité volumique 1 à 8) (représentent τ1
k, τ2
k,..., τ8
k dans les équations du modèle de Maxwell généralisé) |
| Paramètres de l'équation de WLF
|
Température de transition vitreuse
(représente T0 dans l'équation de WLF)
|
|
Première constante pour l'équation de Williams-Landel-Ferry
(représente C1 dans l'équation de WLF)
|
|
Deuxième constante pour l'équation de Williams-Landel-Ferry
(représente C2 dans l'équation de WLF)
|
Lorsque vous définissez une courbe de cisaillement ou de Tables et courbes, le premier point de la courbe est le module G1 ou K1 à l'instant t1. A l'instant t = 0, le programme calcule automatiquement G0 ou K0 à partir du module élastique et du coefficient de Poisson.
Le modèle de matériau viscoélastique peut être utilisé avec des éléments volumiques et de coques épaisses de qualité haute et intermédiaire.
Le temps a des valeurs réelles dans l'analyse non linéaire lorsque vous utilisez le modèle de matériau viscoélastique.