Das System von Bewegungsgleichungen für ein lineares n-Freiheitsgrad-System, erregt durch eine zeitvariierende Kraft ist:
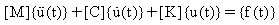(Gleichung 1)
Bei der Verwendung von Koordinatentransformation wird der Satz von n gleichzeitigen Gleichungen auf n unabhängige Gleichungen reduziert (jede Gleichung kann separat gelöst werden):
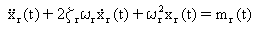für r = 1, 2, ...., n (Gleichung 2)
wobei xr(t) die Schwingungskoordinaten mit Bezug auf die Knotenkoordinaten ur(t) sind durch:
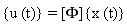(Gleichung 3).
Der Vektor von Schwingungslasten {m(t)} ist angegeben durch:
(Gleichung 4).
Ausgehend davon, dass Erregungen durch Funktionen der spektralen Leistungsdichte (psd) ausgedrückt werden, kann die Lösung in der Frequenzdomäne formuliert werden. Die Erregungs-psd-Matrix ist als [Sf(ω)] gegeben. Die Schwingungskraft-psd-Matrix ist definiert als:
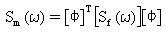(Gleichung 5).
Die spektrale Leistungsdichte der Schwingungsverschiebungsreaktion [Sx(ω)] kommt von:
(Gleichung 6),
wobei [H(ω)] die Schwingungs-Transferfunktionsmatrix und [H*(ω)] ihr komplexes Pendant ist. Bei Normalschwingungen ist die Transferfunktionsmatrix diagonal mit diagonalen Elementen Hr(ω)
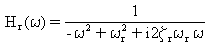(Gleichung 7) und
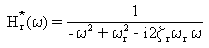(Gleichung 8).
Die Verschiebungsreaktion psd psd [Su(ω)] wird dann von (Gleichung 3) abgeleitet.
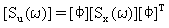(Gleichung 9).
Die spektrale Leistungsdichte der Geschwindigkeits- und Beschleunigungsreaktionen wird ausgedrückt durch:
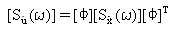(Gleichung 10) und
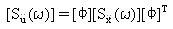(Gleichung 11).
Die spektrale Leistungsdichte der modalen Geschwindigkeit und Beschleunigung steht in Bezug zur spektrale Leistungsdichte der modalen Verschiebung durch:
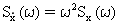(Gleichung 12) und 
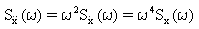(Gleichung 13)
Gleichung 10 und Gleichung 11 können umgeschrieben werden als:
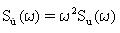(Gleichung 14) und 
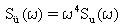(Gleichung 15).
Die modalen Autokorrelationsreaktionen (τ=0) der modalen Reaktion der spektralen Leistungsdichte werden von den Integralen berechnet:
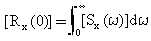(Gleichung 16)
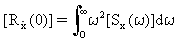(Gleichung 17)
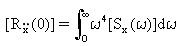(Gleichung 18).
Von den obigen Gleichungen werden die mittleren quadratischen Reaktionen von den diagonalen Werten der Matrizen ermittelt:
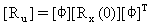(Gleichung 19),
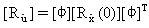(Gleichung 20),
(Gleichung 21).
Quadratische Mittelspannungsreaktion
Die Elementspannungen {σ}werden von den Knotenverschiebungen {u} ermittelt durch:
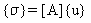(Gleichung 22), oder durch die Modalverschiebungen {x} durch:
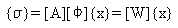(Gleichung 23), wobei [Φ] die Matrix von Eigenvektoren ist.
Die Spannungs-Korrelationsmatrix [Rσ] wird angegeben durch:
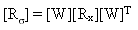(Gleichung 24).