La valutazione del danno da fatica per i componenti che funzionano in un ambiente di vibrazione casuale viene valutata nel dominio della frequenza in base alle proprietà statistiche della funzione PSD (densità spettrale potenza) della sollecitazione di risposta.
Quando le strutture o i componenti meccanici sono soggetti a un modulo di carico casuale, ad esempio una turbina a vento sotto un carico di vento, una piattaforma marina sotto un carico di onde o il motore di un'auto in condizioni stradali diverse, le stime della durata alla fatica sono eseguite nel dominio della frequenza.
Il termine fatica relativa alla vibrazione (o fatica basata sulla frequenza) si riferisce alla stima della durata alla fatica dove il carico e la risposta (cronologie di sollecitazione e deformazione) sono processi casuali e quindi sono meglio descritti utilizzando misure statistiche come la densità spettrale di potenza (funzioni PSD).
Le caratteristiche statistiche della PSD della sollecitazione di risposta possono essere ottenute attraverso i momenti della funzione PSD.
| Caratteristiche statistiche di PSD |
Equazione |
| L'ennesimo momento spettrale della sollecitazione PSD S(f) alla frequenza f (in unità di Hz). |
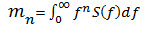 (Eq.1) (Eq.1)
|
| Il valore della radice quadrata media per un processo gaussiano stazionario continuo σ. |
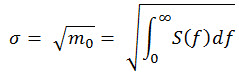 (Eq.2) (Eq.2)
|
| Numero medio di passaggi per lo zero in ascesa E[0] per un tipico campione di 1 secondo. |
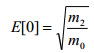 (Eq.3) (Eq.3)
|
| Numero medio di picchi E[p] per un tipico campione di 1 secondo. |
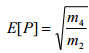 (Eq.4) (Eq.4)
|
| Il fattore di irregolarità γ varia tra 0 e 1. Si avvicina a 1 a mano a mano che il segnale della sollecitazione si avvicina a un processo di banda stretta (per un'onda seno γ = 1). Si avvicina a 0,745 a mano a mano che il segnale della sollecitazione si avvicina a un processo di rumore bianco. |
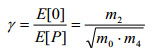 (Eq.5) (Eq.5)
o
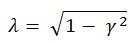 (Eq.6) (Eq.6)
|
Le proprietà della fatica del materiale in genere vengono ottenute da una curva S-N, che definisce la relazione tra il range di sollecitazione, S (questa è la variazione dalla sollecitazione ciclica massima in tensione alla sollecitazione ciclica minima in compressione) rispetto alla media di cicli necessari per produrre il cedimento, N.
Per la maggior parte dei problemi ad alta resistenza alla fatica ciclica (N >= 104), la curva S-N può essere espressa in forma semplificata:
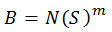 (Eq.7)
(Eq.7)
dove B e M sono le proprietà del materiale che variano con le condizioni di carico e ambientali e sono determinate dagli esperimenti dei test della fatica.
Il danno cumulativo E[AD] dovuto alla fatica da carico casuale si basa sulla regola di Palmgren-Miner ed è espresso nel modo seguente:
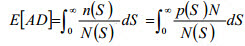 (Eq.8)
(Eq.8)
dove n(S) è il numero di cicli applicati a livello del range di sollecitazione S, p(S) è la funzione di densità della probabilità del range di sollecitazione. Sostituendo l'equazione della curva S-N semplificata nell'equazione di cui sopra, si ottiene un'equazione generale del danno da fatica da risposta alla sollecitazione casuale da:
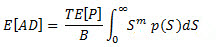 (Eq.9), dove T è la durata in secondi del carico casuale.
(Eq.9), dove T è la durata in secondi del carico casuale.
Sono disponibili tre metodi per la stima del danno da fatica basata sull’Eq.9: il metodo delle tre bande di Steinberg, il metodo della banda stretta e il metodo di Wirshing. Ogni metodo utilizza una definizione diversa per la funzione di densità della probabilità p(S).
Metodo banda stretta
Nel metodo della banda stretta, la funzione di densità della probabilità di picchi per un segnale a banda stretta tende a una distribuzione di Rayleigh (Bendat J. S., Probability Functions for Random Responses. NASA report on Contact NASA-5-4590, 1964).
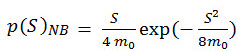 (Eq.10)
(Eq.10)
Sostituzione di (Eq.10) in (Eq.9) e integrazione dei risultati alla seguente espressione per la valutazione del danno da fatica.
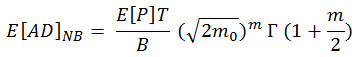 (Eq.11), dove Γ (.) è la funzione gamma.
(Eq.11), dove Γ (.) è la funzione gamma.
Metodo di Wirsching
Il metodo di Wirsching (Wirshing, P.H., Paez, T.L., e Ortiz K., Random Vibration, John Wiley & Sons Inc., New York, 1995) modifica il metodo della banda stretta con un fattore di correzione empirico per prendere in considerazione un processo a banda larga.
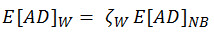 (Eq. 12)
(Eq. 12)
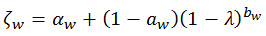 , (Eq. 13)
, (Eq. 13)
ζw è un fattore empirico derivato dalle simulazioni Monte Carlo che comprendono una varietà di funzioni di densità spettrale.
αw e bw sono i parametri di adattamento migliori ottenuti da:
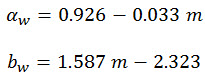 (Eq. 14)
(Eq. 14)
Metodo delle tre bande di Steinberg
L'assunto del metodo di Steinberg è che la funzione di densità della probabilità della risposta alla sollecitazione casuale segue una distribuzione gaussiana e, di conseguenza, i valori previsti delle ampiezze di risposta alla sollecitazione sono vincolati da alcuni livelli di probabilità:
-
il 68,27 % di probabilità che l'ampiezza dei cicli di sollecitazione non ecceda il range di 2 volte il valore della radice quadrata media del segnale di risposta alla sollecitazione.
- il 27,1 % di probabilità che l'ampiezza dei cicli di sollecitazione non ecceda il range di 4 volte il valore della radice quadrata media del segnale di risposta alla sollecitazione.
- il 4,3 % che i cicli di sollecitazione non eccedano il range di 6 volte il valore della radice quadrata media del segnale di risposta alla sollecitazione.
Non si verificano cicli di sollecitazione con range maggiori di 6 volte il valore della radice quadrata media.
Il danno da fatica previsto è dato da:
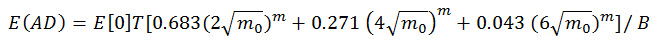 (Eq.15)
(Eq.15)
In Simulation, le funzioni PSD della sollecitazione sono i risultati dello studio dinamico - della vibrazione casuale sul quale si basa lo studio della fatica. Per tutti e tre i metodi viene considerato il componente di sollecitazione vonMises per il calcolo del danno previsto per la fatica.