線形静解析 vs 線形動解析（Linear Static Versus Linear Dynamic Analysis）

線形静解析では荷重は最大の大きさになるまでゆっくりと、そして少しずつかけられます。最大強度に到達後、荷重は一定に保たれます（時間不変）。速度と加速度は微々たるものとされ、慣性力と減衰力は考慮されません。

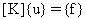
ここで、

[K] :剛性マトリックス

{u}: 変位ベクトル

{f}: 荷重ベクトル

解析では一定の変位と応力が生成されます。

線形動解析では、時間依存の荷重が適用されます。荷重は決定論的（周期性、非周期性）あるいは非決定論的（正確に予測することはできないが統計的に記述可能）に指定できます。速度と加速度は大きな影響をおよぼすため、慣性力と減衰力が考慮されます:

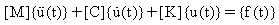
ここで、

[K] :剛性マトリックス

[C] :減衰マトリックス

[M]: 質量マトリックス

{u(t)}:時変変位ベクトル

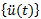: 時変加速度ベクトル

: 時変速度ベクトル

{f(t)}:時変荷重ベクトル

応答は時間履歴 (振幅 vs 時間) か、周波数スペクトル (ピーク値 vs 周波数) で表されます。

線形動的解析では質量、剛性、減衰のマトリックスは時間によって変化しません。

一般的には、荷重周波数が構造の最小固有振動数より大幅に小さい場合は静止状態であると仮定できます。