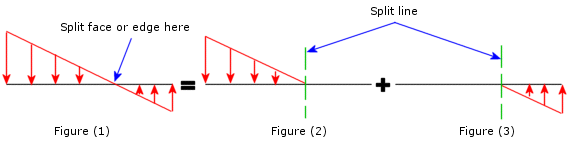
Si se especifica una distribución de manera que las fuerzas cambien la dirección en parte de la arista o cara, como se ilustra en la figura, el programa establece la suma de los valores absolutos de las fuerzas en el mismo valor especificado en el PropertyManager.
|
| Al aplicar una fuerza no uniforme que cambia su dirección [Figura (1)], divida la entidad de carga donde la fuerza cambia su dirección y aplique la fuerza en dos pasos [Figura (2) y Figura (3)].
|