Linear Elastic Isotropic Model
A material is said to be isotropic if its properties do not vary with
direction. Isotropic materials therefore have identical elastic modulus,
Poisson's ratio, coefficient of thermal expansion, thermal conductivity,
etc. in all directions. The term isothermal is some times used to denote
materials with no preferred directions for coefficients of thermal expansion.
In order to define the isotropic elastic properties, you must define
the elastic modulus Ex
. The program
assumes a value of 0.0 for Poisson's ratio nxy,if no
specific value is specified. A
common value for the Poisson's ratio is 0.3. The shear modulus Gxy. is calculated internally by the
program even if it is explicitly specified.
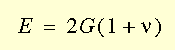
The stiffness matrix for an isotropic material contains only two independent
coefficients. The following sections describe the isotropic stress-strain
relations in two- and three-dimensions including the effect of thermal
strains.
Isotropic Stress-Strain Relations
The most general form of the isotropic stress-strain relations including
thermal effects is shown below:
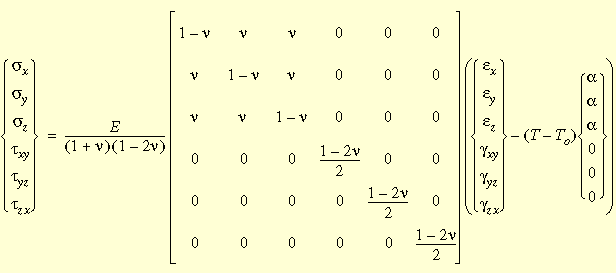
Assumptions of Linear Elastic Material Models
Linear elastic material models make the following assumptions:
Linearity Assumption.
The induced response is directly proportional to the applied loads. For
example, if you double the magnitude of loads, the model's response (displacements,
strains, and stresses) will double. You can make the linearity assumption
if the following conditions are satisfied:
The highest stress
is in the linear range of the stress-strain curve characterized by a straight
line starting from the origin. As the stress increases, materials demonstrate
nonlinear behavior above a certain stress level. This assumption asserts
that the stress should be below this level. Some materials, like rubber,
demonstrate a nonlinear stress-strain relationship even for low stresses.
The maximum displacement
is considerably smaller than the characteristic dimension of the model.
For example, the maximum displacement of a plate must be considerably
smaller than its thickness and the maximum displacement of a beam must
be considerably smaller than the smallest dimension of its cross-section.
Elasticity Assumption.
The loads do not cause any permanent deformation. In other words, the
model is assumed to be perfectly elastic. A perfectly elastic model returns
to its original shape when the loads are removed.
Isotropic
vs. orthotropic materials