In this example, you derive creep constants from reference data for a
Stainless Steel material.
From the Classical Power Law for Creep (Bailey - Norton
law), the creep strain at time t, when no temperature variation is considered, is
given by:
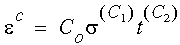
In
the
Material dialog box, the constants C
0, C
1, and C
2 are labeled as:
C0 = Creep
Constant 1, C1 = Creep Constant 2, and C2
= Creep Constant 3
In
the above equation: the Creep Constant 1 (
C0) is calculated in the SI unit system ( stress in N
/m 2 and time in sec), Creep
Constant 2 ( C1 >1) is unitless, and
Creep Constant 3 (C2) is between 0 and 1.
From the reference creep
data below, you calculate the creep constants for the equation of creep state. The
table references constant stress values at constant temperatures that can develop a
creep strain of 1% over an extented period. These data refer to Stainless Steel -
Grade 310.
| Temperature (C) |
Stress (MPa) |
Stress
(MPa) |
| time = 10,000 hr |
time = 100,000
hr |
| 550 |
110 |
90 |
| 600 |
90 |
75 |
| 650 |
70 |
50 |
| 700 |
40 |
30 |
| 750 |
30 |
20 |
| 800 |
15 |
10 |
Select the stress data for temperature 550 C. Assuming C
2 =1, from the creep state equation above, you have a
system of 2 equations with 2 unknowns C
0 and C
1. First you calculate C
1. The
two equations to the state of creep are:
0.01 = C0 * 110 C1* 10,000 (Eq.1)
0.01 = C0 * 90 C1* 100,000 (Eq.2)
Equating the two equations
and using logarithmic functions:
C1 * log (110) = C1 * log (90) +1 (Eq.3)
From (Eq.3), you calculate C1 =
11.47.
You can use either (Eq.1) or (Eq.2) to calculate C0. C0 is calculated in the SI
units, so you need to apply conversion factors.
C0 = 0.01 / ( (90E6)11.47 *
100000 *3600) = 1.616E-102
You enter the three creep constants in the
Material dialog box:
Creep Constant 1 = 1.616E-102 , Creep Constant 2 = 11.47,
Creep Constant 3 = 1
In the
Material dialog box, select Include Creep Effect to activate the creep calculation for the
selected material model. Creep calculations are considered only for nonlinear
studies. Creep effect is not available for the linear elastic orthotropic and
viscoelastic material models.