Modele pełzania
Pełzanie jest zależnym od czasu odkształceniem w stanie stałego naprężenia. Pełzanie obserwuje się w większości materiałów konstrukcyjnych, szczególnie metali w podwyższonych temperaturach, wysoko spolimeryzowanych tworzywach sztucznych, betonie i paliwie stałym w silnikach rakietowych. Ponieważ efekty pełzania wymagają długiego czasu, są one zwykle zaniedbywane w analizie dynamicznej.
Krzywa pełzania przedstawia graf zależności odkształcenia od czasu. Na krzywej pełzania można wyróżnić trzy zakresy pracy: pierwszorzędny, drugorzędny i trzeciorzędny (patrz poniższy rysunek). Zwykle interesuje nas pierwszorzędny i drugorzędny zakres pracy.
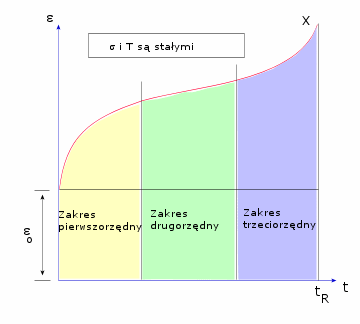
Stosowane są dwa prawa pełzania oparte na „równaniu stanu”. Każde prawo definiuje wyrażenie dla jednoosiowego odkształcenia pełzania w funkcji jednoosiowego naprężenia i czasu.
Klasyczne prawo mocy pełzania (prawo Bailey'a-Nortona)
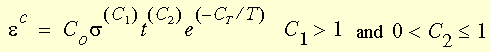
gdzie:
T = Temperatura (Kelwin) (= temperatura wejściowa + temperatura odniesienia + temperatura odsunięcia)
CT = Stała materiałowa definiująca zależność pełzania od temperatury
Klasyczne prawo mocy dla pełzania reprezentuje pierwszorzędny i drugorzędny zakres roboczy w jednym wzorze. Trzeciorzędny zakres roboczy pełzania nie jest rozważany. „t” jest bieżącym czasem rzeczywistym (nie pseudo), a s jest całkowitym naprężeniem jednoosiowym w chwili t.
Aby rozciągnąć te prawa na zachowanie wieloosiowe pełzania, przyjęto następujące założenia:
Prawo pełzania jednoosiowego pozostaje prawidłowe jeżeli odkształcenie pełzania jednoosiowego i naprężenie jednoosiowe zostaną zastąpione ich wartościami skutecznymi.
Materiał jest izotropowy
Odkształcenia pełzania są nieściśliwe
W numerycznej analizie pełzania, gdzie może być stosowane obciążenie cykliczne, w oparciu o regułę umocnienia zgniotowego, bieżące współczynniki odkształcenia pełzania są wyrażone jak funkcje bieżącego naprężenia i całkowitego odkształcenia pełzania:
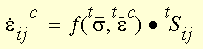
gdzie:
