Model materiału Nitinol

Stopy z pamięcią kształtu (SMA), takie jak Nitinol przejawiają efekty supersprężyste. Termin supersprężyste jest używany do opisania materiałów posiadających zdolność do znacznych deformacji w cyklach obciążania-zwalniania bez widocznych trwałych deformacji. W rzeczywistości w cyklach obciążania-zwalniania, nawet do 10-15% odkształceń, materiał wykazuje reakcję histerezy, ścieżkę sztywne-miękkie-sztywne zarówno dla obciążania i zwalniania, bez trwałej deformacji.

Model materiału Nitinol jest dostępny dla elementów bryłowych i skorupowych.

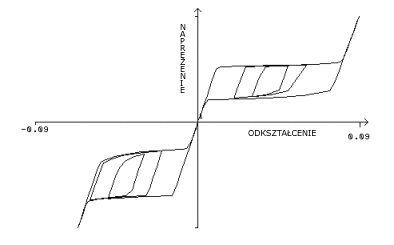
Typowa reakcja rozciągania dla pręta nitinolowego w warunkach obciążenia jednoosiowego. Należy zauważyć, że materiał zachowuje się różnie przy rozciąganiu i ściskaniu.

Krzywa rozciągania stopów z pamięcią kształtu (SMA) demonstruje charakterystyczne zachowanie makroskopowe, nieobecne w tradycyjnych materiałach. Za zachowanie to odpowiadają zjawiska makromechaniczne.

Stopy SMA prezentują odwracalne martenzytowe przekształcenia fazowe, czyli bezdyfuzyjne przekształcenia ciało stałe-ciało stałe pomiędzy fazą o wyższej organizacji krystalograficznej, „austenitem” oraz fazą o niższej organizacji krystalograficznej, „martenzytem”.

Miękkie fragmenty krzywej reakcji reprezentują obszary, gdzie zachodzi przekształcenie fazowe: konwersja austenitu w martenzyt (obciążanie) oraz martenzytu w austenit (zwalnianie).

Dla uproszczenia jednak miękkie zachowanie na krzywej reakcji będziemy nazywać „plastycznym”, a sztywne fragmenty „sprężystymi”.

Według tej definicji, materiał na początku zachowuje się sprężyście, do osiągnięcia pewnego poziomu naprężenia (początkowe naprężenie ustępowania podczas obciążania). Jeżeli obciążanie nadal wzrasta, materiał przejawia zachowania elastoplastyczne, aż do osiągnięcia ostatecznej wartości odkształcenia plastycznego. Od tego punktu, przy zwiększaniu obciążeń materiał zachowuje się ponownie sprężyście.

W przypadku zwalniania, materiał zawsze zaczyna zachowywać się sprężyście, aż do zmniejszenia naprężenia do początkowego naprężenia ustępowania podczas zwalniania. Następnie materiał jest zwalniany w sposób elastoplastyczny, aż do całkowitego zaniku skumulowanego odkształcenia plastycznego (z fazy obciążania). Od teko punktu materiał jest zwalniany sprężyście, aż powróci do swego pierwotnego kształtu (brak trwałej deformacji) i zerowego odkształcenia przy zerowych obciążeniach.

Wyrażenie modelu Nitinol

Ponieważ Nitinol jest zwykle używany ze względu na swą zdolność do podlegania skończonym odkształceniom, do tego modelu stosowana jest teoria dużego odkształcenia wykorzystująca odkształcenia logarytmiczne wraz ze zaktualizowanym wyrażeniem Lagrange'a.

Budowany jest konstytucyjny model wiążący odkształcenia logarytmiczne i komponenty naprężenia Kirchhoffa. Jednakże ostatecznie macierz konstytucyjna i wektor naprężenia są przekształcane tak, by przedstawić naprężenia Cauchy'ego (rzeczywiste).

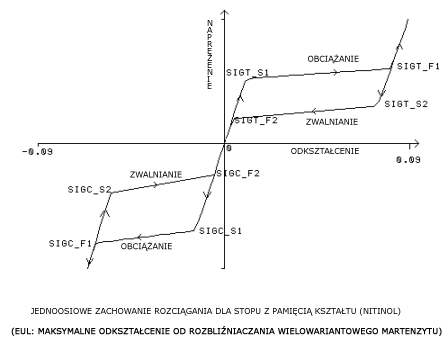
sst1, sft1=Początkowe i końcowe naprężenie ustępowania dla obciążenia rozciągającego. [SIGT_S1, SIGT_F1]

sst2, sft2=Początkowe i końcowe naprężenie ustępowania dla zwalniania rozciągającego. [SIGT_S2, SIGT_F2]

ssc1, sfc1=Początkowe i końcowe naprężenie ustępowania dla obciążenia ściskającego. [SIGC_S1, SIGC_F1]

ssc2, sfc2=Początkowe i końcowe naprężenie ustępowania dla zwalniania ściskającego. [SIGC_S2, SIGC_F2]

eul = (Maksymalne rozciągające odkształcenie plastyczne)(3/2)0.5

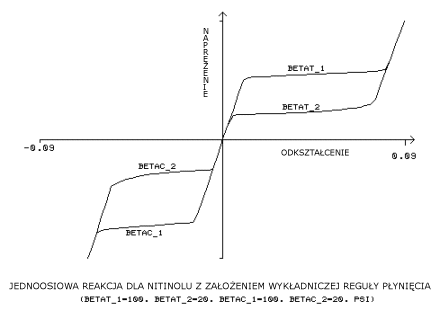
Wykładnicza reguła płynięcia wykorzystuje dodatkowe stałe wejściowe, bt1, bt2, bc1, bc2:

bt1 = parametr materiałowy mierzący szybkość transformacji dla obciążenia rozciągającego, [BETAT_1]

bt2 = parametr materiałowy mierzący szybkość transformacji dla zwalniania rozciągającego, [BETAT_2]

bc1 = parametr materiałowy mierzący szybkość transformacji dla obciążenia ściskającego, [BETAC_1]

bc2 = parametr materiałowy mierzący szybkość transformacji dla zwalniania ściskającego, [BETAC_2]

Kryterium ustępowania

Aby modelować możliwość zależności ciśnieniowej transformacji fazowej, dla kryterium ustępowania użyto funkcji obciążania typu Drucker-Prager:

 F(t) = sqrt(2) s + 3 a p

 F- Rif = 0

gdzie:

s = naprężenie skuteczne

p = naprężenie średnie (lub ciśnienie hydrostatyczne)

a = sqrt(2/3) ( ssc1- sst1) / ( ssc1+ sst1)

Rfi = [ sfi(sqrt (2/3) + a )] : i = 1: obciążanie, i = 2: zwalnianie

Reguła płynięcia

Poprzez wykorzystanie logarytmicznej definicji odkształcenia można prawidłowo wyrazić komponenty dewiatoryjny i wolumetryczny tensorów odkształcenia i naprężenia oraz ich zależności w postaci rozprzężonej.

W pierwszej kolejności rozważmy całkowite wektory odkształcenia plastycznego i sprężystego przedstawione równaniem:

ep = eul xs ( n + a m )

ee = e  - ep

W wyniku tego można obliczyć wektor naprężenia Kirchhoffa ze wzoru:

t = pm + t

p = K ( q - 3 a eulxs)

t = 2G ( e - eul xs n)

W powyższych wyrażeniach:

eul = parametr skalarny reprezentujący maksymalną plastyczną deformację odkształcenia materiału [EUL]

eul = parametr pomiędzy zerem a jednością, będący miarą odkształcenia plastycznego

q =  odkształcenie wolumetryczne = e11 + e22 + e33

e = dewiatoryjny wektor odkształcenia

e = dewiatoryjny wektor naprężenia

n = norma naprężeń dewiatoryjnych: t/(sqrt(2) s) ?

m = macierz identyczności w postaci wektorowej: {1,1,1,0,0,0}T

K & G = współczynniki sprężystości wzdłużnej objętościowy i ścinania: { K = E/[3(1-2n), G = E/[2(1+v)]}

Liniowa reguła płynięcia w postaci inkrementacyjnej możne zostać wyrażona odpowiednio:

Obciążanie: Dxs= ( 1.0 - xs)DF / ( F - R1f)

Zwalnianie: Dxs= xs DF / ( F - R2f)

Wykładnicza reguła płynięcia, używana gdy zdefiniowano niezerowe b:

Obciążanie: Dxs= b1( 1.0 - xs)DF / ( F - R1f)2

Zwalnianie: Dxs= b2xs DF / ( F - R2f)2

Uwagi:

• Generalnie stopy z pamięcią kształtu (SMA) okazują się niewrażliwe na efekty prędkości. Dlatego czas w powyższym wyrażeniu reprezentuje pseudozmienną, a jego długość nie wpływa na rozwiązanie.

• Wszystkie równania przedstawiono tu dla rozciągającego obciążania-zwalniania, ponieważ podobne wyrażenia (z parametrami właściwości ściskania) można wykorzystać dla warunków ściskającego obciążania-zwalniania.

• Inkrementacyjny algorytm rozwiązania wykorzystuje tu procedurę mapowania powrotnego do oszacowania naprężeń i  konstytucyjnych równań dla danego kroku rozwiązania. W związku z tym rozwiązanie składa się z dwóch części. Początkowo obliczany jest stan próbny, a następnie, jeżeli stan próbny narusza kryterium płynięcia, dokonywana jest korekta, aby przywrócić naprężenia do powierzchni płynięcia.

Literatura:

1. Auricchio, F., „A Robust Integration-Algorithm for a Finite-Strain Shape-Memory-Alloy Superelastic Model,” International Journal of Plasticity, vol. 17, pp. 971-990, 2001.

2. Auricchio, F.,  Taylor, R.L., and Lubliner, J., „Shape-Memory-Alloys: Macromodeling and Numerical Simulations of the Superelastic Behavior,”  Computer Methods in Applied Mechanics and Engineering, vol. 146, pp. 281-312, 1997.

3. Bergan, P.G., Bathe, K.J., and Wunderlich, eds. „On Large Strain Elasto-Plastic and Creep Analysis,”  Finite Elements Methods for Nonlinear Problems, Springer-Verlag 1985.

4. Hughes, T., eds. „Numerical Implementation of Constitutive Models: Rate-Independent Deviatoric Plasticity,”  Theoretical Foundation for Large-Scale Computations for Nonlinear Material Behavior, Martinus Nijhoff Publishers, Dordrecht, The Netherlands, 1984.