蠕变模型
蠕变是在恒定应力状态下产生的与时间相关的应变。大多数工程材料,尤其是高温下的金属、高分子塑料、混凝土和火箭发动机中的固体推进剂都会发生蠕变。蠕变效果需要很长的时间才能形成,因此通常在动态分析中被忽略。
蠕变曲线是应变与时间之间的曲线。在蠕变曲线上可以区分三个不同的时段:第一、第二和第三(参阅下图)。通常第一和第二时段较为重要。
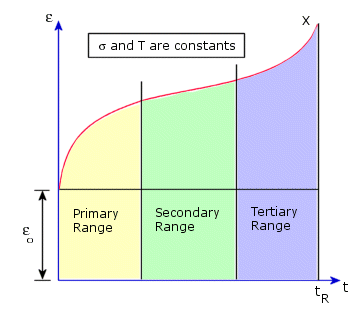
实现基于“状态方程”方法的两种蠕变定律。每种定律按照单轴应力和时间定义了单轴蠕变应变的表达式。
蠕变经典幂定律(Bailey-Norton 定律)
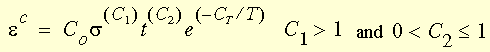
其中:
T = 温度(开氏)(= 输入温度 + 参考温度 + 偏移温度)
CT = 定义蠕变温度相关性的材料常量
蠕变经典幂定律在一个公式中体现了第一和第二蠕变时段。没有考虑第三蠕变时段。“t 是当前实际(而非假定)时间,s 是 t 时刻的总单轴应力。
要将这些定律引伸到多轴蠕变行为,作出以下假设:
对于数值蠕变分析,其中可以应用周期性负载,根据应变硬化规则,当前蠕变应变速率表示为当前应力和总蠕变应变的函数:
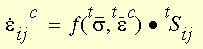
其中:
