粘弹性模型
由于粘性效应而能够消耗机械能的弹性材料具有粘弹性材料的特性。对于多轴应力状态，本构关系可以写成：
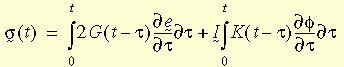
其中 e 和 f 是偏应变和体积应变；G(t - t) 和 K(t - t) 是抗剪弛张函数和整体弛张函数。驰张函数可以由力学模型表示（如此图所示）。通常称为广义麦克斯韦模型，具有以下表达式：
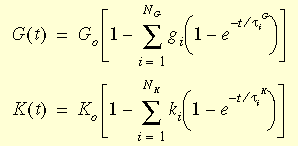
其中 G0 和 K0 是瞬时抗剪和体积模量 (t = 0)，由 G0 =E/2(1+v) 和 K0 =E/3(1-2v) 给出。
gi、ki、tiG、以及 tiK 是第 i 个抗剪和体积模量以及对应的时间。
通过时间-温度对应原理引入了温度对材料行为的影响。此原理的数学形式为：
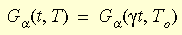
其中 g t 是缩短的时间，g 是转换函数。WLF (Williams-Landel-Ferry) 公式用来近似计算此函数：
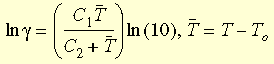
其中 TO 是参考温度，通常被选为玻璃过渡温度；C1 和 C2 是与材料有关的常量。
所需的参数包括以下几项：
|
参数 |
符号 |
说明 |
|
线性弹性参数 |
EX |
弹性模量 |
|
NUxy |
泊松比 |
|
GXY（可选） |
抗剪模量 |
|
驰张函数参数 |
G1，G2，G3，...，G8 |
代表广义麦克斯韦模型公式中的 g1，g2，...，g8 |
|
TAUG1，TAUG2，.....，TAUG8 |
代表广义麦克斯韦模型方程式中的 t1g，t2g，...，t8g |
|
K1，K2，...，K8 |
代表广义麦克斯韦模型公式中的 k1，k2，...，k8 |
|
TAUK1，TAUK2，...，TAUK8 |
代表广义麦克斯韦模型方程式中的 t1k，t2k，...，t8k |
|
WLF 公式参数 |
REFTEMP |
代表 WLF 方程式中的 T0 |
|
VC1 |
代表 WLF 方程式中的 C1 |
|
VC2 |
代表 WLF 方程式中的 C2 |
当在表格与曲线标签下定义抗剪弛张或整体弛张曲线时，曲线的第一个点 G1 或 K1 模态（在时间 t1）。在时间 t = 0，程序自动从弹性模态和普阿松比率计算 G0 或 K0。
粘弹性材料模型可以用于草图和高品质实体以及厚外壳单元。