Inkrementacyjne techniki kontroli
Do celów wykonania analizy nieliniowej opracowano różne techniki kontroli. Techniki te można sklasyfikować następująco:
Inkrementacyjna metoda kontroli obciążenia
W tej strategii obciążenia stosowane w układzie są używane jako zadane zmienne. Każdy stan (punkt) na ścieżce równowagi jest określany przez przecięcie powierzchni (F = stała) ze ścieżką, w celu określenia parametrów deformacji.
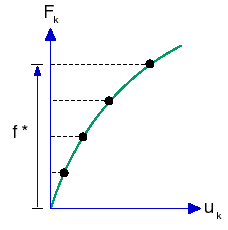
Przy zastosowaniu tej techniki w analizie elementu skończonego, obciążenia (ruchy podstawowe, zadane przemieszczenia, termiczne, grawitacyjne itp.) są stosowane inkrementacyjnie zgodnie ze skojarzonymi krzywymi „czasu”.
Inkrementacyjna metoda kontroli przemieszczenia
W tej technice dany punkt na ścieżce równowagi jest określany przez przecięcie powierzchni zdefiniowanej przez stały parametr przemieszczenia (U = stałe) z krzywą rozwiązania, jak to ukazano na poniższym rysunku.
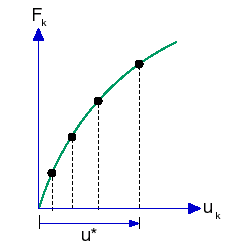
Aby zastosować tą technikę w analizie elementu skończonego, zestaw zastosowanych obciążeń jest inkrementowany proporcjonalnie (przy użyciu pojedynczego mnożnika obciążeń), aby osiągnąć równowagę pod kontrolą określonego stopnia swobody. Kontrolowany stopień swobody, określony przez wybranie wierzchołka lub punktu odniesienia, jest inkrementowany poprzez użycie krzywej „czasu”.
Incremental Arc-Length Control Method
W tej strategii zadawany jest specjalny parametr przy użyciu (pomocniczego) równania powiązania, które jest dodawane do układu równań rządzącego równowagą układu. W sensie geometrycznym parametr kontroli można uznać za „długość łuku” ścieżki równowagi na poniższym rysunku.
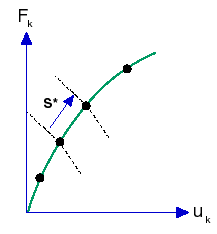
Aby użyć tej techniki w analizie elementu skończonego, zestaw zastosowanych obciążeń jest inkrementowany proporcjonalnie (przy użyciu pojedynczego mnożnika obciążeń), aby osiągnąć równowagę pod kontrolą określonej długości (długości łuku) ścieżki równowagi. Długość łuku zostanie automatycznie obliczona przez oprogramowanie. Nie jest wymagana żadna krzywa czasowa.
Zarówno kontrola siły, jak i kontrola przemieszczenia nie działa w sąsiedztwie punktów zwrotu (znanych jako przeskok dla kontroli siły i przeskok powrotny dla kontroli przemieszczenia, jak na tym rysunku. Trudności te zwykle napotykane są w analizie wyboczenia ram, pierścieni i skorup. Trudności te z powodzeniem pokonuje kontrola długości łuku.
Tematy pokrewne
Procedury numeryczne
Iteracyjne metody rozwiązań dla problemów nieliniowych
Schematy zakończenia
Wykonywanie analizy nieliniowej
Ustawianie właściwości analizy nieliniowej
Ustawianie opcji wyników analizy nieliniowej