Когда использовать динамический анализ

Статические исследования предполагают, что нагрузки являются постоянными или прикладываются весьма медленно до тех пор, пока они не достигают полных значений. Вследствие настоящего допущения скорость и ускорение каждой частицы модели принимаются нулевыми. В результате, статические исследования пренебрегают инерционными силами и силами демпфирования.

Во многих практических случаях нагрузки не прикладываются медленно или они изменяются со временем или по частоте. Для таких случаев используйте динамическое исследование. В общем, если частота нагрузки больше чем 1/3 самой низкой (основной) частоты, следует использовать динамическое исследование.

Линейные динамические исследования базируются на частотных исследованиях. Программное обеспечение рассчитывает реакцию модели посредством сложения влияний каждой моды на среду нагрузки. В большинстве случаев, только нижние моды вносят значительный вклад в реакцию. Влияние моды зависит от частотного спектра нагрузки, величины, направления, продолжительности и местоположения.

Цели динамического анализа включают:

• Проектирование структурных и механических систем для работы без разрушения в динамических средах.

• Модификация характеристик системы (то есть, формы, механизмов демпфирования, свойств материала, и т. п.), чтобы уменьшить влияние вибрации.

Уравнения движения

Системы с одной степенью свободы (SDOF)

Рассмотрим простую упругую систему с массами. Масса (m) подвергнута воздействию силы F(t) в направлении u в качестве функции времени. Масса может перемещаться только в направлении u и, следовательно, является системой с одной степенью свободы (SDOF). Движению сопротивляется пружина жесткостью (к).

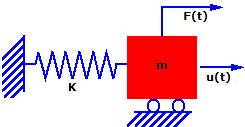
Записывая второй закон Ньютона (сила равна массе умноженной на ускорение) для этой системы во время (t), получаем:

F(t)-ku(t) = mu..(t)

или:

mu..(t) + ku(t) = F(t)

где:

u..(t) – ускорение массы во время (t) и оно равно второй производной u относительно времени.

k = жесткость пружины

Теоретически, если масса смещена и освобождена, она будет продолжать колебаться с одинаковой амплитудой нескончаемо долгий период времени. На практике, масса вибрирует с постепенно уменьшающейся амплитудой до тех пор, пока не придет в состояние покоя. Настоящее явление называется демпфированием и оно вызывается потерей энергии посредством трения и других влияний. Демпфирование является сложным явлением. В целях настоящего обсуждения, предполагаем, что демпфирующая сила пропорциональна скорости. Настоящий вид демпфирования называется вязкостное демпфирование.

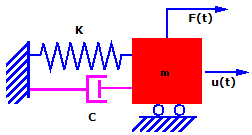
С учетом демпфирования вышеприведенное уравнение становится:

mu..(t) + cu.(t) + ku(t) = F(t)

где:

u.(t) – скорость массы во время (t) и оно равно первой производной u относительно времени.

Примечание: В статических исследованиях скорость и ускорение так малы, что ими можно пренебречь, а F и u не являются функциями времени. Вышеприведенное уравнение уменьшается до: F=ku.

Системы со многими степенями свободы (MDOF)

Для систем со многими степенями свободы (MDOF) m, c и k становятся матрицами, а не одиночными значениями и уравнения движения выражены как:

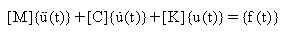, где

[M]: матрица масс

[K] : матрица жесткости

[C] : матрица демпфирования

{u(t)}: вектор перемещения во время t (составляющие перемещения каждого узла)

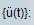вектор ускорения во время t (ускорение компонентов каждого узла)

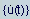вектор скорости во время t (скорость компонентов каждого узла)

{f(t)}: изменяющийся во времени вектор нагрузки (сила компонентов каждого узла)

Связанные разделы

Линейный статистический в сравнении с линейным динамическим анализом

Динамические нагрузки

Нагрузки и параметры вывода результатов динамического анализа