Model materiálu Nitinol

Slitina s tvarovou pamětí (SMA), například Nitinol, demonstruje tzv. superelastický efekt. Termín superelastický se používá pro popis materiálů se schopností podstoupit velké deformace v cyklech zatížení-odlehčení bez projevů trvalých deformací. Ve skutečnosti, v cyklech zatížení-odlehčení, při namáhání až 10-15 %, materiál projevuje hysterezní odezvu, průběh tuhý-měkký-tuhý pro zatížení a odlehčení a žádnou trvalou deformaci.

Model materiálu Nitinol je dostupný objemové prvky a prvky skořepiny.

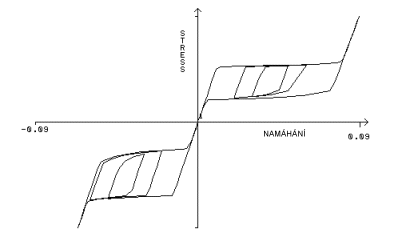
Typická odezva zatížení-odlehčení pro niklo-titanovou tyč pod podmínkami jednoosého zatížení. Všimněte si, že materiál se chová jinak v tahu a v tlaku

Křivka závislosti mezi napětím a namáháním pro slitiny s tvarovou pamětí projevuje zřetelné makroskopické chování, které se nevyskytuje v tradičních materiálech. Toto chování přisuzováno vnitřním makromechanismům.

Slitina s tvarovou pamětí (SMA) má reverzibilní martenzitové fázové změny, neboli přechody mezi vyšší krystalografickou fází („austenit“) a krystalografickou podřazenou fází („martenzit“).

Měkké části křivky odezvy znázorňují oblasti s fázovým přechodem: změnou austenitu na martenzit (zatížení) a martenzitu na austenit (odlehčení).

Pro zjednodušení však budeme měkké chování na křivce odezvy označovat jako „plastické“ a tuhé části jako „elastické“.

Podle této definice se materiál nejprve chová elasticky, než dosáhne určité úrovně napětí (počáteční mez kluzu). Pokud zatížení pokračuje, materiál projevuje elastoplatické chování, než plastické namáhání dosáhne hodnoty své meze. Dále se materiál bude pod zvýšenými zatíženími znovu chovat elasticky.

Při odlehčení se materiál vždy začne odlehčovat elasticky, než je napětí sníženo na počáteční mez kluzu při odlehčení. Materiál se pak bude odlehčovat elastoplastickým způsobem, než se všechno nahromaděné plastické namáhání (z fáze zatížení) vytratí. Od tohoto bodu dál, se materiál bude odlehčovat elasticky, než se vrátí do původního tvaru (bez trvalé deformace) a nulového namáhání pod nulovým zatížením.

Formulace modelu Nitinol

Vzhledem k tomu, že Nitinol se většinou používá pro svou schopnost podstoupit konečná namáhání, pro tento model se používá teorie velkého namáhání využívající aktualizovanou Langrangeovu formulaci.

Základní model je tudíž vytvořen s ohledem na logaritmická zatížení a Kirchhoffovy prvky napětí. Základní matice a vektor napětí jsou však nakonec převedeny na existující Cauchyho (pravá) napětí.

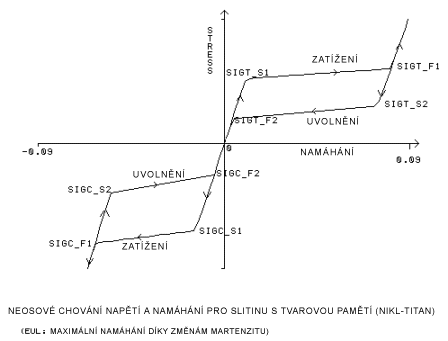
sst1, sft1=Počáteční a koncová mez kluzu pro zatížení v tahu. [SIGT_S1, SIGT_F1]

sst2, sft2=Počáteční a koncová mez kluzu pro odlehčení v tahu. [SIGT_S2, SIGT_F2]

ssc1, sfc1=Počáteční a koncová mez kluzu pro zatížení tlakem. [SIGC_S1, SIGC_F1]

ssc2, sfc2=Počáteční a koncová mez kluzu pro odlehčení tlakem. [SIGC_S2, SIGC_F2]

eul = (Maximální tahové napětí plastu)(3/2)0,5

Pravidlo exponenciálního toku využívá další vstupní konstanty, bt1, bt2, bc1, bc2:

bt1 = parametr materiálu měřicí rychlost transformace pro zatížení v tahu, [BETAT_1]

bt2 = parametr materiálu měřicí rychlost transformace pro odlehčení v tahu, [BETAT_2]

bc1 = parametr materiálu měřicí rychlost transformace pro zatížení tlakem, [BETAC_1]

bc2 = parametr materiálu měřicí rychlost transformace pro odlehčení tlakem, [BETAC_2]

Kritérium tažnosti

Chcete-li modelovat možnost tlakové závislosti fázové transformace, pro kritérium tažnosti je použita funkce zatížení typu Drucker-Prager:

 F(t) = sqrt(2) s + 3 a p

 F- Rif = 0

Kde:

s = účinné napětí

p = střední napětí (nebo hydrostatický tlak)

a = sqrt(2/3) ( ssc1- sst1) / ( ssc1+ sst1)

Rfi = [ sfi(sqrt (2/3) + a )] : i = 1: zatížení, i = 2: odlehčení

Pravidlo průtoku

Zavedením logaritmické definice namáhání mohou být výchylkové a objemové součásti namáhání a tenzory napětí a jejich vztahy správně vyjádřeny.

Nejprve uvážíme vektory celkového plastické a elastického namáhání reprezentované následovně:

ep = eul xs ( n + a m )

ee = e  - ep

V důsledku toho bude Kirchhoffův vektor napětí vypočten jako:

t = pm + t

p = K ( q - 3 a eulxs)

t = 2G ( e - eul xs n)

Ve formulacích výše:

eul = ?skalární parametr představující maximální plastickou deformaci materiálu v tahu [EUL]

xs = ?parametr mezi nula & jedna, jako míra plastického namáhání

q =  objemové namáhání = e11 + e22 + e33

e = vektor výchylkového namáhání

t = vektor výchylkového napětí

n = norma výchylkového napětí: t/(sqrt(2) s) ?

m = matice identifikátoru ve vektorové formě: {1,1,1,0,0,0}T

K & G = hromadný a smykový modul pružnosti: { K = E/[3(1-2n), G = E/[2(1+v)]}

Pravidlo lineárního toku v přírůstkové formě může být vyjádřeno následovně:

Zatížení: Dxs= ( 1,0 - xs)DF / ( F - R1f)

Odlehčení: Dxs= xs DF / ( F - R2f)

Pravidlo exponenciálního toku používané pro nenulové b je definováno následovně:

Zatížení: Dxs= b1( 1,0 - xs)DF / ( F - R1f)2

Odlehčení: Dxs= b2xs DF / ( F - R2f)2

Poznámky:

• Slitiny s tvarovou pamětí se obecně považují za necitlivé k poměrným účinkům. Ve výše uvedené formulaci tudíž „čas“ představuje pseudoproměnnou a jeho délka neovlivňuje řešení.

• Všechny rovnice jsou zde uvedeny pro zatížení-odlehčení v tahu, protože podobné výrazy (s tlakovými parametry) je možné použit pro podmínky zatížení-odlehčení tlakem.

• Přírůstkový algoritmus řešení zde používá postup zpětného mapování při hodnocení napětí a  základních rovnic pro krok řešení. Řešení se tedy skládá ze dvou částí. Nejprve je vypočítán dočasný stav; pokud potom dočasný stav nesplňuje kritérium toku, je provedena taková úprava, aby se napětí vrátila na plochu toku.

Odkazy:

1. Auricchio, F., “A Robust Integration-Algorithm for a Finite-Strain Shape-Memory-Alloy Superelastic Model,” International Journal of Plasticity, vol. 17, s. 971-990, 2001.

2. Auricchio, F.,  Taylor, R.L., a Lubliner, J., “Shape-Memory-Alloys: Macromodeling and Numerical Simulations of the Superelastic Behavior,”  Computer Methods in Applied Mechanics and Engineering, vol. 146, s. 281-312, 1997.

3. Bergan, P.G., Bathe, K.J., a Wunderlich, eds. “On Large Strain Elasto-Plastic and Creep Analysis,”  Finite Elements Methods for Nonlinear Problems, Springer-Verlag 1985.

4. Hughes, T., eds. “Numerical Implementation of Constitutive Models: Rate-Independent Deviatoric Plasticity,”  Theoretical Foundation for Large-Scale Computations for Nonlinear Material Behavior, Martinus Nijhoff Publishers, Dordrecht, The Netherlands, 1984.