Modelo de plasticidad de von Mises
El criterio de flexibilidad se escribe de esta forma:
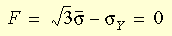
donde s es la tensión efectiva y sY es el límite elástico de las pruebas uniaxiales. El modelo von Mises se puede utilizar para describir el comportamiento de los metales. Al utilizar este modelo de material, debe considerarse lo siguiente:
Se supone la existencia de plasticidad con una deformación unitaria pequeña cuando se utiliza un desplazamiento pequeño o grande.
Se crea una suposición de regla de flujo asociada.
Hay reglas de endurecimiento isotrópico y cinemático disponibles. Se implementa una combinación lineal de endurecimiento isotrópico y cinemático cuando tanto el radio como el centro de la superficie elástica en espacio desviatorio pueden variar con respecto al historial de carga.
El parámetro RK define la proporción de endurecimiento cinemático e isotrópico.
Para endurecimiento isotrópico, el parámetro RK tiene el valor 0. El radio de la superficie elástica se expande pero su centro permanece fijo en espacio desviatorio.
Para endurecimiento cinemático, el parámetro RK tiene el valor 1. El radio de la superficie elástica permanece constante mientras su centro se mueve en espacio desviatorio.
Se puede introducir una curva de tensión-deformación unitaria para plasticidad bilineal o multilineal. Para la definición de la curva de tensión-deformación unitaria bilineal, se utiliza el cuadro de diálogo Material para introducir el límite elástico y el módulo elástico. Para la definición de la curva de tensión-deformación unitaria multilineal, debe definirse una curva de tensión-deformación unitaria.
Al definirse una curva de tensión-deformación unitaria, el primer punto de la curva debe ser el punto de flexibilidad del material. Las propiedades de material, como el módulo elástico, límite elástico, etc. se obtendrán de la curva de tensión-deformación unitaria cuando la misma se encuentre disponible y no de la tabla de propiedades de material, en el cuadro de diálogo Material. Sólo se tomará de la tabla el coeficiente de Poisson (NUXY).
Los estudios de caída no admiten la definición de curvas de tensión-deformación unitaria.
Los parámetros SIGYLD y ETAN para la descripción de la curva de tensión-deformación unitaria bilineal pueden asociarse con las curvas de temperatura para llevar a cabo análisis termoplásticos.
Se recomienda el uso del método iterativo NR (Newton-Raphson).
El modelo de Huber-von Mises puede utilizarse con los elementos de vaciado sólido y grueso (de calidad alta y de borrador).
La termoplasticidad no está disponible con los elementos de vaciado.
La siguiente figura ilustra una curva de tensión-deformación unitaria típica de un material plástico:
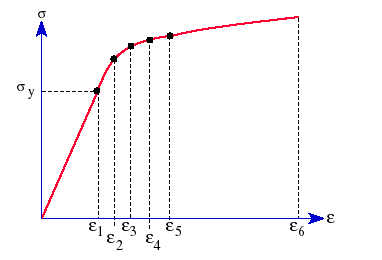
Análisis de grandes deformaciones unitarias
En la teoría de la plasticidad de grandes deformaciones unitarias, una medida de deformación unitaria logarítmica se define como:
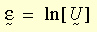
donde U es el tensor de estiramiento derecho que generalmente se obtiene de la descomposición polar derecha del gradiente de deformación F (es decir, F = R U, R es el tensor de rotación). La deformación unitaria logarítmica incremental se estima de la siguiente manera:
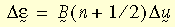
donde B (n+1/2) es la matriz de deformación unitaria-desplazamiento estimada en el paso de la solución n+1/2 y Du es el vector de desplazamientos incrementales. Es preciso tener en cuenta que la forma anterior es una aproximación de segundo orden a la fórmula exacta.
La velocidad de tensión se toma de la velocidad de Green-Naghdi para que el modelo constitutivo sea objetivo y no produzca variaciones en las imágenes. Al transformar la velocidad de tensión del sistema global al sistema R:
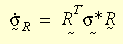
El modelo constitutivo completo tendrá una forma idéntica a la teoría de pequeñas deformaciones unitarias. La teoría de plasticidad de grandes deformaciones unitarias se aplica al criterio de flexibilidad de von Mises, a la regla de flujo asociativo y al endurecimiento isotrópico o cinemático (bilineal o multilineal). El endurecimiento bilineal admite la dependencia de la temperatura de la propiedad de material. En el caso actual, se utiliza el algoritmo radial o de retorno. La idea básica consiste en aproximarse al vector normal N mediante:
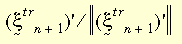
donde:
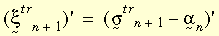
La siguiente figura ilustra las dos ecuaciones anteriores.
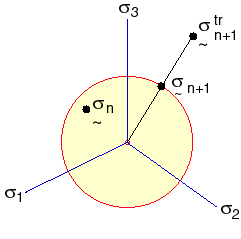
El vector de fuerza y las matrices de rigidez de los elementos se calculan según la fórmula lagrangiana actualizada. Las tensiones de Cauchy, las deformaciones unitarias logarítmicas y el espesor actual (sólo elementos de vaciado) se registran en el archivo de resultados.
La elasticidad en el caso actual se modela en una forma hiperelástica que supone la existencia de deformaciones unitarias elásticas pequeñas, pero admite deformaciones unitarias plásticas arbitrariamente grandes. Para problemas de elasticidad con deformaciones unitarias grandes (como el caucho), puede utilizar modelos de material hiperelástico como Mooney-Rivlin.
Debe utilizarse la tensión (verdadera) de Cauchy y la deformación unitaria logarítmica para la definición de la curva de tensión-deformación unitaria multilineal.
Comparación de criterios de plasticidad de Tresca y von Mises