Modely tečení
Tečení je časově závislé namáhání vzniklé za stavu konstantního napětí. Tečení bylo pozorováno ve většině materiálů, zvláště kovech za vyšší teploty, plastech vyšších polymerů, betonu a pevných palivech v raketových motorech. Vzhledem k tomu, že vznik tečení trvá dlouho, v dynamické analýze se jeho vlivy většinou zanedbávají.
Křivka tečení je graf namáhání v čase. V křivce tečení je možné rozpoznat tři různé režimy; první, druhý a třetí (viz následující obrázek). Zájem je většinou a primární a sekundární režimy.
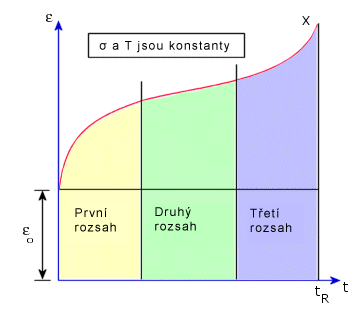
Na základě přístupu „rovnice stavu“ jsou zavedeny dva zákony tečení. Každý zákon definuje výraz pro jednoosé namáhání tečení za podmínek jednoosého napětí a času.
Klasický zákon síly pro tečení (zákon Bailey-Norton)

kde:
T = Teplota (Kelvin) (= vstupní teplota + referenční teplota + odchylka teploty)
C
T = Konstanta materiálu určující závislost tečení na teplotě
C0 je Konstanta tečení 1, která se zadává na kartě Vlastnosti v dialogovém okně Materiál.
Konstanta tečení 1 musí mít zadané jednotky v systému SI. Koeficient převodu se rovná 1/ (napětí ^ (C1) * čas ^ (C2)). Jednotky napětí jsou v N/m2 a čas je v sekundách.
C1 je Konstanta tečení 2 a C2 je Konstanta tečení 3 v dialogovém okně s vlastnostmi materiálů.
Klasický zákon síly pro tečení představuje primární a sekundární režimy tečení v jednom vzorci. Terciární režim tečení se neuvažuje. “t“ je aktuální skutečný (ne pseudo) čas a sigma je celkové jednoosé napětí v čase t.
Aby tyto zákony platily pro chování víceosého tečení, vychází se z následujících předpokladů:
-
Zákon jednoosého tečení zůstává platný v případě, že jednoosé namáhání tečením a jednoosé napětí jsou nahrazeny svými efektivními hodnotami.
-
Materiál je izotropní
-
Namáhání při tečení jsou nestlačitelná
U numerické analýzy tečení, kde může být použito cyklické zatěžování, jsou podle pravidla tvrzení poměry aktuálního namáhání tečením vyjádřeny funkce aktuálního napětí a celkového namáhání tečením:

kde:
