Model plasticity Tresca
Toto kritérium je založeno na předpokladu, že ve stavu deformace je maximální smykové napětí ve všech bodech média stejné a že je rovno polovině meze kluzu, která se získá z testu jednoosého tahu pro daný materiál.
V trojrozměrném případě dojde k deformaci v případě, že platí alespoň jedna z nerovností:

Deformace je tedy založena na maximálním smykovém napětí, které je rovno polovině rozdílu maximálního a minimálního hlavního napětí. Podle tohoto kritéria neovlivňuje střední hlavní napětí stav deformace.
Intenzita smykového napětí
Intenzita smykového napětí je definována druhou odmocninou druhé invarianty odchylky napětí a lze ji vyjádřit jako:
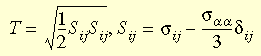
Stav úplného smyku
Stav úplného smyku je definován jako:

U tohoto stavu je intenzita smykového napětí a maximální smykové napětí ekvivalentní:
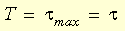
Pomocí podmínek Tresca se smykové napětí v bodu deformace určí jako polovina tahové meze kluzu:

Podle kritéria tažnosti von Mises odpovídá smyková mez kluzu tomuto vztahu:

Poznámky
-
U modelu Tresca jsou k dispozici pravidla izotropního a kinematického tvrzení. Lineární kombinace izotropního a kinematického tvrzení se použije v případě, že se poloměr a střed povrchu deformace v prostoru odchylek může vzhledem k vývoji zatížení lišit.
-
Parametr RK definuje poměr kinematického a izotropního tvrzení.
-
U zcela izotropního tvrzení má parametr RK hodnotu 0. Poloměr povrchu deformace se zvětší, ale střed zůstává v prostoru na stejném místě.
-
U zcela kinematického tvrzení má parametr RK hodnotu 1. Poloměr povrchu deformace zůstává stejný, zatímco střed se v prostoru může pohybovat.
Porovnání kritérií Tresca a von Mises pro plasticitu