Modèle viscoélastique
Les matériaux élastiques qui ont la capacité de dissiper de l'énergie mécanique à cause d'effets visqueux sont qualifiés de matériaux viscoélastiques. Pour l'état de contraintes multi-axiales, la relation constitutive peut être exprimée ainsi :
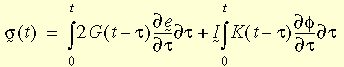
où e et f sont des déformations déviatoriques et volumétriques ; G(t - t
) et K(t - t
) sont des fonctions de cisaillement et d'élasticité volumique en relaxation. Les fonctions de relaxation peuvent être représentées par le modèle mécanique (montré dans cette figure
) généralement appelé modèle Maxwell généralisé et ayant les expressions suivantes :
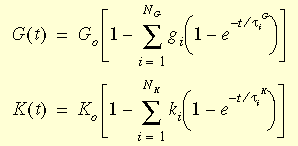
où G
0 et K
0 sont les modules de cisaillement et d'élasticité volumique initiaux (t = 0) obtenus ainsi : G
0
bsp;
= E/2(1+v) et K
0
bsp;
= E/3(1-2v).
g
i, k
i, t
i
G et t
i
K sont les i-ème modules de cisaillement et d'élasticité volumique et leurs temps correspondants.
L'effet de la température sur le comportement du matériau est basé sur le principe de correspondance temps-température. L'expression mathématique du principe est la suivante :
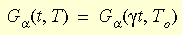
où g t représente le temps réduit et g la fonction de décalage. L'équation de WLF (Williams-Landel-Ferry) permet d'approcher la fonction :
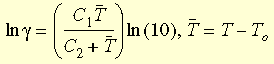
où T
O représente la température de référence généralement choisie comme température de transition de Glass ; C1 et C2 sont des constantes dépendant du matériau.
Les paramètres requis sont :
|
Paramètre
|
Symbole
|
Description
|
|
Paramètres linéaires élastiques
|
EX
|
Module d'élasticité
|
|
NUxy
|
Coefficient de Poisson
|
|
GXY (optionnel)
|
Module de cisaillement
|
|
Paramètres de fonctions de relaxation
|
G1, G2, G3,..., G8
|
représentent g1, g2, ...,g8 dans les équations du modèle de Maxwell généralisé
|
|
TAUG1, TAUG2, ....., TAUG8
|
représentent t
1
g, t
2
g,..., t
8
g dans les équations du modèle Maxwell généralisé
|
|
K1, K2, ..., K8
|
représentent k1, k2, ...,k8 dans les équations du modèle de Maxwell généralisé
|
|
TAUK1, TAUK2, ..., TAUK8
|
représentent t
1
k, t
2
k,..., t
8
k dans les équations du modèle Maxwell généralisé
|
|
Paramètres de l'équation de WLF
|
REFTEMP
|
représente T0 dans l'équation de WLF
|
|
VC1
|
représente C1 dans l'équation de WLF
|
|
VC2
|
représente C2 dans l'équation de WLF
|
Lors de la définition d'une courbe de relaxation de cisaillement ou d'élasticité volumique dans l'onglet Tables & Courbes, le premier point de la courbe est le module G
1
bsp;
ou K
1
bsp;
à l'instant t
1. A l'instant t = 0, le programme calcule automatiquement G
0
bsp;
ou K
0 à partir du module élastique et du coefficient de Poisson.
Le modèle de matériau viscoélastique peut être utilisé avec des éléments volumiques et de coques épaisses de qualité haute et intermédiaire.