塑性 von Mises 模型

屈服准则可以写成下列形式：

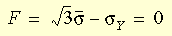
其中 s 是有效应力，sY 是单轴测试的屈服应力。von Mises 模型可以用来描述金属的行为。在使用这种材料模型时，应该注意以下事项：

• 当使用小型位移和大型位移时，假设小应变塑性。

• 作相关流动规则假设。

• 同向性和运动性硬化规则均可用。当偏量空间中的屈服曲面的半径和中心可以相对于载荷历史而变化时，将实施同向性和运动性硬化的线性组合。

参数 RK 定义运动性硬化和同向性硬化的比例。

对于纯同向性硬化，参数 RK 的值为 0。屈服曲面的半径扩展，但其中心让固定在偏量空间中。

对于纯运动性硬化，参数 RK 的值为 1。屈服曲面的半径保持不变，但其中心可在偏量空间中移动。

• 可以输入塑性的双线性 或多线性单轴应力-应变曲线。对于双线性应力-应变曲线定义，通过材料对话框输入屈服强度和弹性模量。对于多线性应力-应变曲线定义，应该定义应力-应变曲线。

• 当定义应力-应变曲线时，曲线时的第一个点应该是材料的屈服点。弹性模量、屈服强度等材料属性将取自应力-应变曲线（如果有），而不是取自材料对话框中的材料属性表。只有泊松比 (NUXY) 将取自此表。

掉落测试算例不支持定义应力-应变曲线。

• 双线性应力-应变曲线说明的屈服强度和弹性模量参数可以与温度曲线相关联来执行热塑性分析。

• 建议使用 NR（牛顿拉夫森）迭代方法。

Huber-von Mises 模型可以用于实体（草图和高品质）以及厚壳体（草图和高品质）单元。

热塑性不适用于壳体单元。

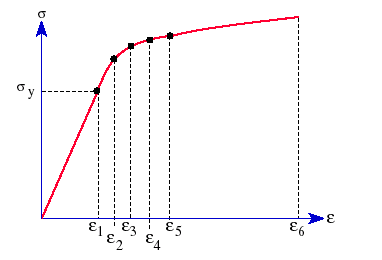
下图描述塑性材料的典型应力-应变曲线：

大型应变分析

在大型应变塑性理论中，对数应变测量定义为：

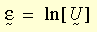
其中 U 是从变形梯度 F 的右极分解得到的右伸展张量（即 F = R U，R 是旋转张量）。增量对数应变估计为：

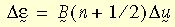
其中 B (n+1/2) 是在 n+1/2 处估计的应变-位移矩阵，D u 是增量位移向量。可以注意到，上述形式是对精确公式的二阶近似。

应力速率可以看作 Green-Naghdi 速率，以使本构模型的框架恰当地不变或客观。通过将应力速率从全局系统变换至 R 系统，

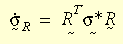
整个本构模型在形式上与小型应变理论相同。大型应变塑性理论适用于 von Mises 屈服准则、相关流动规则以及同向性或运动性硬化（双线性或多线性）。双线性硬化支持材料属性的温度依赖性。当前情况下会用到径向-返回算法。基本思想是通过下式近似法向向量 N：

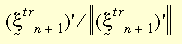
其中：

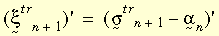
下图说明以上两个公式。

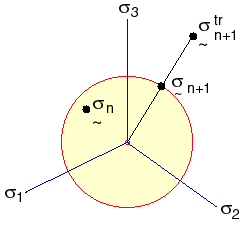
单元力向量和刚度矩阵是根据更新的拉格朗日公式计算。Cauchy 应力、对数应变和当前厚度（仅壳体单元）记录在输出文件中。

当前情况下的弹性用超弹性形式建模，其中假设了小型弹性应变，但允许任意的大型塑性应变。对于大型应变弹性问题（类似橡胶），可以使用超弹性材料模型，如 Mooney-Rivlin。

在定义多线性应力-应变曲线时，应该使用 Cauchy（真实）应力和对数应变。

Tresca 和 von Mises 塑性准则的比较