Mean Stress Correction
The alternating stress amplitude for a stress cycle is computed as half the stress range in the cycle. The amount of damage caused by a stress cycle depends not only on the alternating stress but also on the mean stress. For example, the two cycles below have the same alternating stress but because they have different mean stresses, they cause different amounts of damage.
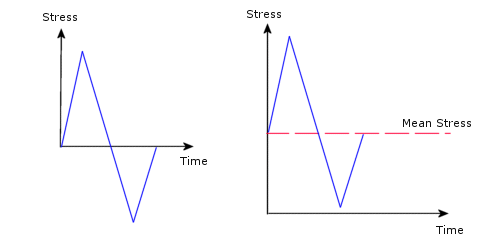
The effect of mean stresses on the cycles to failure is illustrated by the following diagram, called the Haigh diagram.

The mean stress is zero only when the load is fully reversible. The most straightforward case is when an S-N curve with the same R-ratio as the loading is provided. In this case, the S-N curve is directly used since no correction is needed. If you define S-N curves with different R-ratios, the software accounts for the mean stress by linear interpolation between the curves. If only one S-N curve with an R-ratio that is different from the R-ratio of the loading is provided, a correction is needed.
 The program always uses the von Mises stress to calculate the mean stress. Since von Mises is a positive quantity, the program assigns the sign of the first mean principal stress to it for the purpose of calculating the associated mean stress.
The program always uses the von Mises stress to calculate the mean stress. Since von Mises is a positive quantity, the program assigns the sign of the first mean principal stress to it for the purpose of calculating the associated mean stress.
Definitions
To discuss correction methods, let us define the following variables for a stress cycle:
Smax = maximum stress
Smin = minimum stress
DS = stress range = Smax- Smin
Sa = alternating stress = (Smax - Smin)/2
Smean = mean stress = (Smax + Smin)/2
R = Stress ratio = Smin/Smax
A = amplitude ratio = Sa/Smean
The stress and amplitude ratios for some common loadings are listed:
|
Loading Type
|
Stress and Amplitude Ratios
|
|
Fully reversed
|
R = -1, A = infinity
|
|
Zero to maximum
|
R = 0, A = 1
|
|
Zero to Minimum
|
R = infinity, A = -1
|
Correction methods
In the following let:
Sca = the corrected alternating stress (based on zero mean.),
Sy = yield stress, and
Su = ultimate strength
The software offers the following methods to calculate Sca:
|
Method
|
Equation
|
|
1. Goodman method- generally suitable for brittle materials:
|
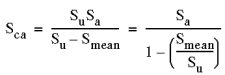
|
|
2. Gerber method - generally suitable for ductile materials
|
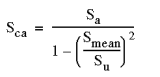
|
|
3. Soderberg method - generally the most conservative
|
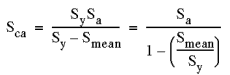
|
For both variable and constant amplitude events, the software calculates the mean stress in addition to the alternating stress for each cycle and then it evaluates the corrected stress using the specified criteria.
Related Topics
Definitions
Evaluation of Alternating Stresses From Constant Amplitude Fatigue Events
Performing Fatigue Analysis
S-N Curve
Fatigue Plots