Von-Mises-Verformbarkeitsmodell

Die Fließkriterien können wie folgt definiert werden:

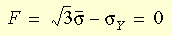
Dabei ist s die Wirkspannung und s Y die Fließspannung aus uniaxialen Tests. Das von-Mises-Modell kann zum Beschreiben des Verhaltens von Metallen verwendet werden. Bei der Verwendung dieses Materialmodells müssen folgende Überlegungen beachtet werden:

• Verformbarkeit bei geringer Dehnung wird angenommen, wenn kleine oder große Verschiebungen verwendet werden.

• Es wird eine zugehörige Fließregelannahme getroffen.

• Sowohl isotrope als auch kinematische Erhärtungsregeln sind verfügbar. Eine lineare Kombination isotroper und kinematischer Erhärtung wird implementiert, wenn der Radius und die Mitte der Streckoberfläche in abweichendem Raum hinsichtlich der Belastungshistorie variieren können.

Der Parameter RK definiert die Proportion kinematischer und isotroper Erhärtung.

Für rein isotrope Erhärtung hat der Parameter RK den Wert 0. Der Radius der Streckoberfläche nimmt zu aber die Mitte bleibt im abweichenden Raum fixiert.

Für rein kinematische Erhärtung hat der Parameter RK den Wert 1. Der Radius der Streckoberfläche bleibt konstant während die Mitte im abweichenden Raum beweglich ist.

• Eine bilineare oder multilineare uniaxiale Spannungs-Dehnungskurve für Verformbarkeit kann eingegeben werden. Für die bilineare Spannungs-Dehnungskurven-Definition werden die Fließgrenze und das Elastizitätsmodul im Dialogfeld Material eingegeben. Für die multilineare Spannungs-Dehnungskurven-Definition sollte eine Spannungs-Dehnungskurve definiert werden.

• Wenn Sie eine Spannungs-Dehnungs-Kurve definieren, sollte der erste Punkt auf der Kurve der Fließpunkt des Materials sein. Materialeigenschaften wie Elastizitätsmodul, Fließgrenze usw. werden der Spannungs-Dehnungskurve entnommen, wenn sie verfügbar ist, und nicht der Tabelle mit den Materialeigenschaften im Dialogfeld Material. Lediglich die Poissonsche Zahl (NUXY) stammt aus dieser Tabelle.

In Fallprüfungsstudien wird die Definition von Spannungs-Dehnungskurven nicht unterstützt.

• Die Parameter Fließspannung und Elastizitätsmodul für die Beschreibung der bilinearen Spannungs-Dehnungskurve können mit Temperaturkurven verbunden werden, um die thermoplastische Analyse durchzuführen.

• Der Einsatz der iterativen NR (Newton-Raphson)-Methode wird empfohlen.

Das Huber-von Mises-Modell kann mit Volumenkörperelementen (Entwurf und hohe Qualität) und dickwandigen Schalenelementen (Entwurf und hohe Qualität) verwendet werden.

Thermoplastizität ist für Schalenelemente nicht verfügbar.

Nachfolgend ist eine typische Spannungs-Dehnungskurve eines verformbaren Materials dargestellt:

Analyse großer Dehnungen

In der Theorie der Analyse großer Dehnungen ist ein logarithmisches Dehnungsmaß wie folgt definiert:

wobei U der rechte Dehnungstensor ist, in der Regel erhalten aus der rechten polaren Änderung des Verformungsgradienten F (d.h. F = R U, R ist der Rotationstensor). Die inkrementelle logarithmische Dehnung wird angenähert als:

wobei B (n+1/2) die Dehnung-Verschiebungsmatrix ist, geschätzt bei n+1/2, und D u der inkrementelle Verschiebungsfaktor ist. Es wird vermerkt, dass die obige Form eine Näherung zweiter Ordnung der exakten Formel ist.

Als Spannungsrate wird die Green-Naghdi-Rate verwendet, damit das konstitutive Modell entsprechend rahmen-invariant oder objektiv wird. Durch Umwandeln der Spannungsrate aus dem globalen System in das R-System,

Das gesamte konstitutive Modell wird formidentisch mit der Theorie für kleine Dehnungen sein. Die Plastizitätstheorie für große Dehnungen wird auf die von-Mises-Fließkriterien, zugehörige Fließregel und isotrope oder kinematische Erhärtung (bilinear oder multilinear) angewendet. Die Temperaturabhängigkeit der Materialeigenschaften wird durch die bilineare Erhärtung unterstützt. Der radiale Erholungsalgorithmus wird im aktuellen Fall verwendet. Die grundlegende Idee ist die Annäherung des Normalvektors N durch:

Dabei gilt Folgendes:

In der folgenden Abbildung sind die beiden oben genannten Gleichungen dargestellt.

Der Elementkraftvektor und die Steifigkeitsmatrizen werden auf Basis der aktualisierten Lagrange-Formel berechnet. Die Cauchy-Spannungen, logarithmischen Dehnungen und aktuellen Dicken (nur Schalenelemente) werden in der Ausgabedatei aufgezeichnet.

Die Elastizität im aktuellen Fall wird in der hyperelastischen Form moduliert, die kleine elastische Dehnungen erwartet, jedoch zufällige große plastische Dehnungen gestattet. Bei Elastizitätsproblemen mit großer Dehnung (gummiartig) können hyperelastische Materialmodelle, wie Mooney-Rivlin, verwendet werden.

Cauchy-Spannung (wahre) und logarithmische Dehnung sollten zur Definition der multilinearen Spannungs-Dehnungskurve verwendet werden.

Vergleich der Tresca- und von-Mises-Kriterien für Verformbarkeit