Linear elastisches orthotropes Modell

Im Gegensatz zu einem isotropen Material hat ein orthotropes Material bevorzugte Festigkeitsrichtungen, die im rechten Winkel zueinander stehen. Die Eigenschaften entlang dieser Richtungen (auch als Hauptrichtungen bezeichnet) sind die Grenzwerte der Elastizitätskoeffizienten. Die [D]-Matrix für ein orthotropes Material hat neun unabhängige elastische Eigenschaften. Außerdem gibt es drei Eigenschaften für die Wärmeausdehnung.

Zweidimensionales orthotropes Spannungs-Dehnungsverhältnis

In zwei Dimensionen kann das Spannungs-Dehnungsverhältnis wie folgt definiert werden (einschl. Temperaturauswirkungen):

bsp;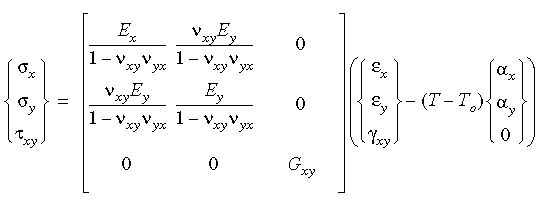

Es ist zu beachten, dass zum Erhalt von Symmetrie in der Matrix des Elastizitätsmoduls Folgendes gilt: n xy E y = n yx E x.

Es muss daher die obige Symmetriebedingung erfüllt werden, wenn Sie die numerischen Werte des Elastizitätsmoduls oder die Poissonsche Zahl eingeben.

Wenn Sie den numerischen Wert des Schubmoduls nicht eingeben, berechnet das Programm diesen wie nachstehend gezeigt:

bsp;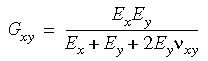

In drei Dimensionen schreiben die orthotropen Symmetriebedingungen Folgendes vor:

bsp;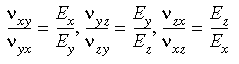

Wenn Sie die orthotropen Materialeigenschaften in drei Dimensionen eingeben, müssen Sie daher sicherstellen, dass die obigen Symmetriebedingungen nicht verletzt werden. Wenn Sie die numerischen Werte des Schubmoduls nicht eingeben, berechnet das Programm diese wie nachstehend gezeigt:

bsp;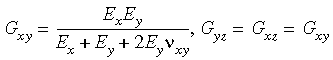

Wenn E x = E y = E z, bsp;berechnet das Programm die Schubmodule intern, auch wenn diese explizit definiert sind. Das Programm nimmt 0,0 für Poissonsche Zahlen an, die nicht explizit definiert sind.

Vergleich isotroper und orthotroper Materialien