Viskoelastisches Modell
Elastische Materialien, die die Fähigkeit haben, die mechanische Energie aufgrund von Viskositätseffekten zu verteilen, werden als viskoelastische Materialien bezeichnet. Bei mehrachsigen Spannungszuständen kann der konstitutive Zusammenhang wie folgt ausgedrückt werden:
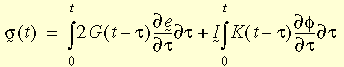
Dabei sind e und f die deviatorische und volumetrische Dehnung; G(t - t
) und K(t - t
) sind Schub- und Umgebungsentspannungsfunktionen. Die Entspannungsfunktionen können dann durch das mechanische Modell dargestellt werden (gezeigt in dieser Abbildung
), das in der Regel als verallgemeinertes Maxwell-Modell bezeichnet wird und folgende Gleichungen hat:
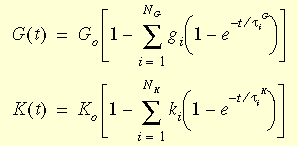
wobei G
0 und K
0 die initialen Schub- und Umgebungsmodule (t = 0) sind bei: G
0
bsp;
= E/2(1+v) und K
0
bsp;
= E/3(1-2v).
g
i, k
i, t
i
G, und t
i
K sind die i-ten Schub- und Umgebungsmodule und zugehörigen Zeiten.
Die Auswirkung der Temperatur auf das Materialverhalten wird durch das Zeit-Temperatur-Korrespondenzprinzip berücksichtigt. Die mathematische Form dieses Prinzips lautet:
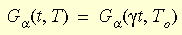
Dabei ist g t die reduzierte Zeit und g die Versatzfunktion. Die WLF-Gleichung (Williams-Landel-Ferry) dient zur Annäherung der Funktion:
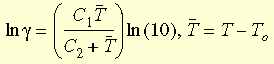
Dabei ist TO die Referenztemperatur, die in der Regel als Glasübergangstemperatur verwendet wird; C1 und C2 sind materialabhängige Konstanten.
Zu den erforderlichen Parametern gehören:
|
Parameter
|
Symbol
|
Beschreibung
|
|
Linear elastische Parameter
|
EX
|
Elastizitätsmodul
|
|
NUxy
|
Poissonsche Zahl
|
|
GXY (optional)
|
Schubmodul
|
|
Entspannungsfunktionsparameter
|
G1, G2, G3,..., G8
|
stellen g1, g2, ...,g8 in den Gleichungen des verallgemeinerten Maxwell-Modells dar
|
|
TAUG1, TAUG2, ....., TAUG8
|
stellen t
1
g, t
2
g,..., t
8
g in den Gleichungen des verallgemeinerten Maxwell-Modells dar
|
|
K1, K2, ..., K8
|
stellen k1, k2, ...,k8 in den Gleichungen des verallgemeinerten Maxwell-Modells dar
|
|
TAUK1, TAUK2, ..., TAUK8
|
stellen t
1
k, t
2
k,..., t
8
k in den Gleichungen des verallgemeinerten Maxwell-Modells dar
|
|
WLF-Gleichungsparameter
|
REFTEMP
|
stellt T0 in der WLF-Gleichung dar
|
|
VC1
|
stellt C1 in der WLF-Gleichung dar
|
|
VC2
|
stellt C2 in der WLF-Gleichung dar
|
Wenn Sie eine Schub- und Umgebungsrelaxationskurve auf der Registerkarte Tabellen & Kurven definieren, ist der erste Punkt der Kurve das Modul G
1
bzw. das Modul K
1
zur Zeit t
1. Zur Zeit t = 0 berechnet das Programm automatisch G
0
oder K
0 aus dem Elastizitätsmodul und der Poissonschen Zahl.
Das viskoelastische Materialmodell kann für Volumenkörper- und dickwandige Schalenelemente mit hoher und Entwurfsqualität verwendet werden.