Modelo do material nitinol
As ligas com memória de forma (SMA), como as de nitinol, apresentam o efeito superelástico. O termo superelástico é usado para descrever materiais com capacidade de passar por grandes distorções em ciclos de carga e descarga sem apresentar distorções permanentes. De fato, sob ciclos de carga e descarga, mesmo com deformações de 10 a 15%, o material apresenta uma resposta histerética e uma memória de caminho duro-macio-duro, tanto no carregamento quanto no descarregamento, sem distorções permanentes.
O modelo de material Nitinol está disponível para elementos sólidos e de casca.
|
|
|
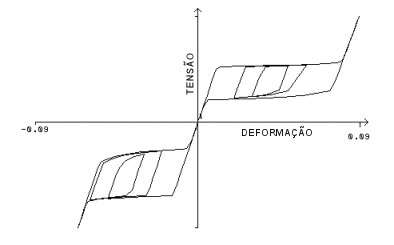
Uma resposta típica de tensão-deformação de uma barra de nitinol sob condições de carregamento uniaxial. Note que o material comporta-se diferentemente na tensão e na compressão.
|
A curva de tensão-deformação de ligas com memória de forma demonstra um comportamento macroscópico distinto que não é apresentado por outros materiais tradicionais. Esse comportamento é atribuído à macromecânica subjacente.
A SMA apresenta uma fase de transformações martensíticas reversíveis; isto é, transformações sólido-sólido sem difusão entre uma fase "austenita", mais organizada cristalograficamente, e uma fase "martensita", menos organizada cristalograficamente.
As partes da curva indicando resposta suave representam as áreas onde uma transformação de fase: a conversão de austenita em martensita (carregamento, e de martensita para austenita (descarregamento).
Entretanto, por uma questão de simplicidade, faremos referência ao comportamento suave na curva de resposta como "plástico" e nas partes duras, como "elástico".
De acordo com essa definição, o material se comporta de forma elástica até que um determinado nível de tensão seja alcançado (limite de tensão inicial no carregamento). Se o carregamento continua, o material apresenta comportamento elastoplástico até que a deformação plástica atinja o valor máximo. Deste ponto em diante, o material se comportará novamente de maneira elástica, sob cargas aumentadas.
Durante a descarga, novamente o material começará a descarregar elasticamente até que a tensão seja reduzida ao limite inicial de escoamento no descarregamento. O material descarregará então de forma elastoplástica, até que toda a deformação plástica acumulada (na fase de carregamento) seja perdida. Deste ponto em diante, o material descarregará elasticamente até retornar à sua forma original (nenhuma distorção permanente) e à tensão zero sob cargas zero.
Fórmula do modelo de nitinol
Como o nitinol geralmente é usado pela sua capacidade de suportar deformações finitas, para este modelo é empregada a teoria de grandes deformações usando deformações logarítmicas com a fórmula de Lagrange atualizada.
O modelo constitutivo é, portanto, construído para relacionar as deformações logarítmicas e os componentes de tensão de Kirchhoff. Entretanto, no fim do processo, a matriz constitutiva e o vetor de tensão serão transformados para apresentar as tensões (verdadeiras) de Cauchy.
s
s
t1
, s
f
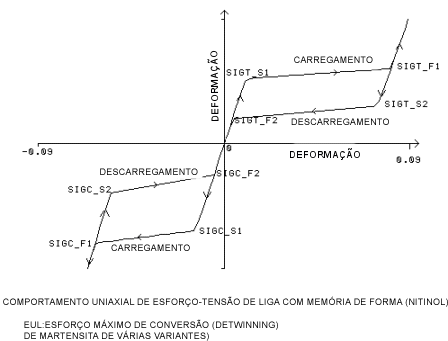
t1 = Limites inicial e final de escoamento para a carga de tração. [SIGT_S1, SIGT_F1]
s
s
t2
, s
f
t2 = Limites inicial e final de escoamento para o descarregamento de tensão. [SIGT_S2, SIGT_F2]
s
s
c
1
, s
f
c
1 = Limites inicial e final de escoamento para o carregamento com compressão. [SIGC_S1, SIGC_F1]
s
s
c2
, s
f
c2 = Limites inicial e final de escoamento para o descarregamento de compressão. [SIGC_S2, SIGC_F2]
eul = (deformação plástica de tensão máxima)(3/2)0,5

A lei do fluxo exponencial usa as constantes adicionais de entrada, b
t1, b
t2, b
c1, b
c2:
bt1 = parâmetro de material, medição da velocidade de transformação para a carga de tração, [BETAT_1]
bt2 = parâmetro de material, medição da velocidade de transformação para o descarregamento de tensão, [BETAT_2]
bc1 = parâmetro de material, medição da velocidade de transformação para o carregamento de compressão, [BETAC_1]
bc2 = parâmetro de material, medição da velocidade de transformação para o descarregamento de compressão, [BETAC_2]
Critério de resistência
Para modelar a possibilidade da dependência da pressão da transformação de fase, é utilizada uma função de carregamento do tipo Drucker-Prager para o critério de resistência:
bsp;
F(
t
) = sqrt(2) s + 3 a p
bsp;F- Rif = 0
Onde:
s = tensão eficaz
p = tensão média (ou pressão hidrostática)
a = sqrt(2/3) ( s
s
c
1
- s
s
t1
) / ( s
s
c
1 + s
s
t1
)
R
f
i = [ s
f
i ( sqrt (2/3) + a )] : i = 1: carregamento, i = 2: descarregamento
A regra do fluxo
Por meio da adoção da definição de deformação logarítmica, os componentes desviadores e volumétricos dos tensores de tensão e deformação e suas relações podem ser expressos corretamente em separado.
Primeiramente, consideremos os vetores totais das deformações plásticas e elásticas representadas por:
e
p = e
ul x
s ( n + a m )
e
e = e
bsp;- e
p
Como resultado, o vetor de tensão de Kirchhoff pode ser avaliado por:
t = p m + t
p = K ( q - 3 a e
ul x
s
)
t = 2G ( e - e
ul x
s n)
Nas fórmulas acima:
eul = parâmetro escalar representando a distorção máxima da deformação plástica do material [EUL].
xs = parâmetro entre zero e um, como uma medida da deformação plástica.
q = bsp;deformação volumétrica = e
11 + e
22 + e
33
e = vetor de deformação desviatória
e = vetor de deformação desviatória
n = norma da tensão desviadora: t
/(
sqrt(2) s
)
m = matriz identidade em forma de vetor: {1,1,1,0,0,0}T
K & G = módulos elásticos de volume e de cisalhamento: { K = E/[3(1-2n), G = E/[2(1+v)]}
A regra do fluxo linear na forma incremental pode ser expressa, consequentemente:
Carregamento: Dx
s = ( 1.0 - x
s
) D
F / ( F - R
1
f
)
Descarregamento: Dx
s = x
s D
F / ( F - R
2
f
)
E a regra de fluxo exponencial, usada quando um b diferente de zero é definido:
Carregamento: Dx
s = b
1 ( 1.0 - x
s
) D
F / ( F - R
1
f
)
2
Descarregamento: Dx
s = b
2 x
s D
F / ( F - R
2
f
)
2
Notas:
• Em geral, ligas com memória de forma são insensíveis aos efeitos de taxas. Assim, na fórmula acima, o "tempo" representa uma pseudovariável e sua duração não influi na solução.
• Todas as equações são apresentadas aqui para carregamento e descarregamento da tração, pois expressões semelhantes (com parâmetros de propriedades compressivas) podem ser usadas para condições compressivas de carregamento e descarregamento.
• O algoritmo de solução incremental usa aqui um procedimento de diretrizes de retorno na avaliação de tensões, e bsp;equações constitutivas para uma etapa de solução. Consequentemente, a solução consiste em duas partes: De início, é feito um cálculo de teste; se a tentativa violar o critério de fluxo, é feito um ajuste para o retorno às tensões da superfície do fluxo.
Referências:
1. Auricchio, F., "A Robust Integration-Algorithm for a Finite-Strain Shape-Memory-Alloy Superelastic Model", International Journal of Plasticity, vol. 17, pp. 971-990, 2001.
2. Auricchio, F., bsp;Taylor, R.L. e Lubliner, J., “Shape-Memory-Alloys: Macromodeling and Numerical Simulations of the Superelastic Behavior,” bsp;Computer Methods in Applied Mechanics and Engineering, vol. 146, pp. 281-312, 1997.
3. Bergan, P.G., Bathe, K.J., and Wunderlich, eds. “On Large Strain Elasto-Plastic and Creep Analysis,” bsp;Finite Elements Methods for Nonlinear Problems, Springer-Verlag 1985.
4. Hughes, T., eds. "Numerical Implementation of Constitutive Models: Rate-Independent Deviatoric Plasticity,” bsp;Theoretical Foundation for Large-Scale Computations for Nonlinear Material Behavior, Martinus Nijhoff Publishers, Dordrecht, Holanda, 1984.