Modelo viscoelástico
Os materiais elásticos, tendo a capacidade de dissipar a energia mecânica devido aos efeitos viscosos, são caracterizados como materiais viscoelásticos. Para estados de tensão multiaxial, a relação constitutiva pode ser escrita como:
onde e e f são as deformações desviatórias e volumétricas; G(t - t
) e K(t - t
) são as funções de relaxamento de cisalhamento e em massa. As funções de relaxamento podem então ser representadas pelo modelo mecânico (mostrado nesta figura
), geralmente um modelo generalizado de Maxwell com expressões como:
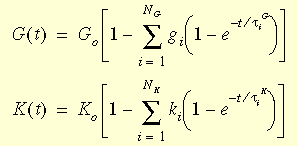
onde G
0 e K
0 são os módulos de cisalhamento e de volume iniciais (t = 0) dados por: G
0
bsp;
= E/2(1+v) e K
0
bsp;
= E/3(1-2v).
g
i, k
i, t
i
G e t
i
K são os i-ésimos módulos de cisalhamento e volume e seus tempos correspondentes.
O efeito da temperatura no comportamento do material é introduzido mediante o princípio de correspondência entre o tempo e a temperatura. A forma matemática do princípio é:
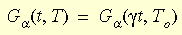
onde g t é a duração reduzida e g é a função de troca. A equação de Williams-Landel-Ferry (WLF) é utilizada para aproximação da função.
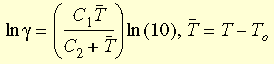
onde TO é a temperatura de referência geralmente escolhida como temperatura de transição do vidro, C1 e C2 são constantes dependentes de material.
Os parâmetros necessários incluem:
|
Parâmetro
|
Símbolo
|
Descrição
|
|
Parâmetros elásticos lineares
|
EX
|
Módulo elástico
|
|
NUxy
|
Coeficiente de Poisson
|
|
GXY (opcional)
|
Módulo de cisalhamento
|
|
Parâmetros da função relaxamento
|
G1, G2, G3,..., G8
|
representam g1, g2, ...,g8 nas equações do Modelo de Maxwell Generalizado.
|
|
TAUG1, TAUG2, ....., TAUG8
|
representam t
1
g, t
2
g,..., t
8
g nas equações do Modelo Generalizado de Maxwell
|
|
K1, K2, ..., K8
|
representam k1, k2, ...,k8 nas equações do Modelo Generalizado de Maxwell.
|
|
TAUK1, TAUK2, ..., TAUK8
|
representam t
1
k, t
2
k,..., t
8
k nas equações do Modelo de Maxwell Generalizado.
|
|
Parâmetros da equação WLF
|
REFTEMP
|
representa T0 na equação WLF
|
|
VC1
|
representa C1 na equação WLF
|
|
VC2
|
representa C2 na equação WLF
|
Ao definir a curva de relaxamento de cisalhamento ou em massa na guia Tabelas e curvas, o primeiro ponto da curva é o módulo G
1
bsp;
ou K
1
bsp;
no momento t
1. No momento t = 0, o programa calcula automaticamente G
0
bsp;
ou K
0 a partir do Módulo elástico e do Coeficiente de Poisson.
O modelo de material viscoelástico pode ser usado para elementos de casca espessa ou sólida, de qualidade alta ou de rascunho.