Modelo ortotrópico elástico linear

Em contraste com um material isotrópico, um material ortotrópico tem direções preferidas de forças, que são mutuamente perpendiculares. As propriedades ao longo dessas direções (também conhecidas como direções principais) são os valores extremos dos coeficientes elásticos. A matriz [D] para um material ortotrópico tem nove propriedades elásticas independentes. Além disso existem três propriedades para a expansão térmica.

Relações tensão-deformação ortotrópicas em 2D

Em duas dimensões, as relações tensão-deformação ortotrópicas podem ser escritas como a seguir, incluindo os efeitos da temperatura:

bsp;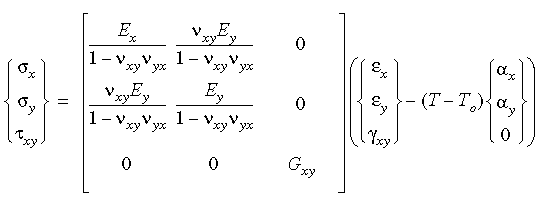

Note que para satisfazer a simetria na matriz dos módulos elásticos, nxyEy = nyx Ex.

Você precisa satisfazer a condição de simetria anterior ao informar os valores numéricos do módulo elástico ou do Coeficiente de Poisson.

Além disso, se você não inserir o valor numérico do módulo de cisalhamento, o programa o calculará da forma a seguir:

bsp;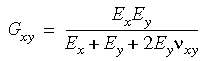

Em três dimensões as condições de simetria ortotrópica exigem que:

bsp;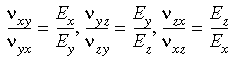

Portanto, ao dar entrada nas propriedades ortotrópicas do material, você deve se certificar que as condições de simetria acima não sejam violadas. Note que se você não der entrada nos valores numéricos dos módulos de cisalhamento, o programa os calculará usando as relações mostradas abaixo:

bsp;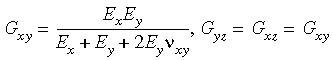

Se E x = E y = E z, bsp;o programa calcula o módulo de cisalhamento internamente, mesmo que ele seja definido explicitamente. O programa pressupõe 0,0 para os coeficientes de Poisson que não sejam explicitamente definidos.

Materiais isotrópicos X materiais ortotrópicos