Quando usar análise dinâmica

Os estudos estáticos assumem que as cargas são constantes ou aplicadas muito lentamente até atingirem o valor máximo. Devido a isso, a velocidade e a aceleração de cada partícula do modelo são consideradas iguais a zero. Como resultado, os estudos estáticos ignoram as forças inerciais e de amortecimento.

Em muitos casos práticos, as cargas não são aplicadas lentamente ou se alteram com o tempo ou com a frequência. Nesses casos, utilize um estudo dinâmico. Geralmente, se a frequência de uma carga for maior do que 1/3 da menor frequência (fundamental), deve-se usar um estudo dinâmico.

Os estudos dinâmicos lineares se baseiam em estudos de frequência. O software calcula a resposta do modelo através da soma da contribuição de cada modo para o ambiente de carregamento. Na maioria dos casos, os modos inferiores contribuem significativamente para a resposta. A contribuição de um modo depende do conteúdo de frequência, da magnitude, da direção, da duração e da localização da carga.

Os objetivos de uma análise dinâmica incluem:

• Projetar sistemas estruturais e mecânicos para trabalharem sem falhas em ambientes dinâmicos.

• Modificar características do sistema (p.ex., geometria, mecanismos de amortecimento, propriedades de material, etc.) para reduzir os efeitos da vibração.

Equações de movimento

Sistema com um grau de liberdade (SDOF)

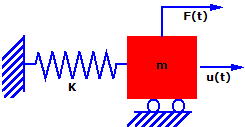
Considere um sistema simples massa-mola. A massa (m) está sujeita a uma força F(t) na direção u em função do tempo. A massa pode se mover somente na direção u e, portanto, este é um sistema com um grau de liberdade (SDOF). O movimento é contrariado por uma mola com rigidez (k)

.

Aplicando a segunda lei de Newton (força igual a massa vezes a aceleração) a esse sistema no instante (t), obtemos:

F(t)-ku(t) = mu..(t)

ou:

mu..(t) + ku(t) = F(t)

onde:

u..(t) é a aceleração da massa no instante (t), sendo igual à derivada segunda de u em relação ao tempo

k = é a rigidez da mola

Teoricamente, se a massa for deslocada e liberada, ele continuará a vibrar com a mesma amplitude para sempre. Na prática, a massa vibra com amplitudes progressivamente menores até o repouso. Esse fenômeno se chama amortecimento e é causado pela perda de energia através do atrito e de outros efeitos. O amortecimento é um fenômeno complexo. Nesta discussão, assumiremos que a força de amortecimento é proporcional à velocidade. Esse tipo de amortecimento é chamado de amortecimento viscoso.

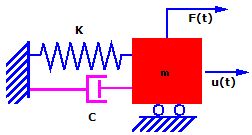
Considerando o amortecimento, as equações acima se tornam:

mu..(t) + cu.(t) + ku(t) = F(t)

onde:

u..(t) é a velocidade da massa no instante (t), sendo igual à derivada primeira de u em relação ao tempo

Nota: Em estudos estáticos, a velocidade e a aceleração são tão pequenas que podem ser desprezadas, e F e u não são funções do tempo. A equação acima se reduz a: F = ku.

Sistema com múltiplos graus de liberdade (MDOF)

Em um sistema com múltiplos graus de liberdade (MDOF), m, c, e k se tornam matrizes em vez de valores únicos e as equações do movimento são:

, onde

[M]: matriz de massa

[K] : matriz de rigidez

[C] : matriz de amortecimento

{u(t)}: vetor do deslocamento no instante t (componentes do deslocamento de todos os nós)

vetor da aceleração no instante t (componentes da aceleração de todos os nós)

vetor da velocidade no instante t (componentes da velocidade de todos os nós)

{f(t)}: vetor de carga com variação no tempo (componentes da força de todos os nós)

Tópicos relacionados

Análise estática linear comparada com análise dinâmica linear

Cargas dinâmicas

Cargas e opções de resultado para análise dinâmica