Analysis Procedure - Random Vibration

The system of equations of motion for a linear n degree-of-freedom system excited by a time varying force is:

(Equation 1)

Using coordinate transformation, the set of n simultaneous equations reduces to n independent equations (each equation can be solved independently):

for  r = 1, 2, ...., n (Equation 2)

where xr(t) are the modal coordinates related to the nodal coordinates ur(t) by:

(Equation 3).

The vector of modal loads {m(t)} is given by:

  (Equation 4).

Assuming that excitations are expressed by their power spectral density (psd) functions, the solution can be formulated in the frequency domain. If the excitation psd matrix is given as [Sf(w)], the modal force psd matrix is defined as:

(Equation 5).

The psd of the modal displacement response [Sx(w)] is obtained from:

(Equation 6),

where [H(w)] is the modal transfer function matrix, and [H*(w)] is its complex conjugate. For normal modes, the transfer function matrix is diagonal with diagonal elements Hr(w)

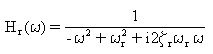(Equation 7) and (Equation 8).

The displacement response psd [Su(w)] is then derived from (Equation 3).

(Equation 9).

The psd of the velocity and acceleration responses are expressed by:

(Equation 10), and

  (Equation 11).

The modal velocity and acceleration psd are related to the modal displacement psd by:

(Equation 12), and (Equation 13)

Equation 10 and Equation  11 can be rewritten as:

(Equation 14) and (Equation 15).

The zero delay modal autocorrelation responses (t=0) in terms of the modal response psd are calculated from the integrals:

  (Equation 16)

(Equation 17)

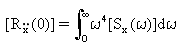(Equation 18).

From the above equations, the mean square responses are determined from the diagonal terms of the matrices:

(Equation 19),

(Equation 20),

(Equation 21).

Stress Mean Square Response

The element stresses {s} are determined from the nodal displacements {u} by:

(Equation 22), or in terms of the modal displacements {x} by:

(Equation 23), where [F] is the matrix of eigenvectors.

The stress correlation matrix [Rs] is given by:

(Equation 24).

Related Topics

Modal Analysis

Random Vibration Analysis

Definitions