Blatz-Ko 應變能密度函數很適合用來塑建可壓縮聚醯胺發泡類型的橡膠模型,可以下式表示:
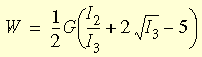
其中:
- G = E / 2(1+ν) 是在無限變形下的剪力模數,E 是彈性的楊氏係數,ν 是 Poisson 比
- Ik (k=1、..3) 是 C=Ik ©) 的不變量,C 是 Cauchy-Green 變形張量
- C = 2ε +I,ε 是 Lagrangian 應變張量,而 I 是單位矩陣。
上述表達式中僅包含一個材料常數 G。由於 Blatz-Ko 模型的 ν = 0.25,唯一能納入考量的材料屬性只有楊氏係數。
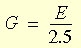
目前只有純實體元素 (粗略及精細品質) 的元素可支援 Blatz-Ko 模型。
所選的 Blatz-Ko 模型是將 Blatz 和 Ko (1962) 所證得的表達式加以簡化後的形式,用來塑建高度可壓縮聚醯胺發泡橡膠的變形模式。應變能大致上如下列表達式:
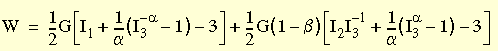
其中
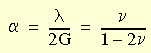
彈性位勢的此三參數族的特定形式是由後來的學者提出,其中將下列常數 α、β 及 ν 的值假設為:α = 0.5、β = 0 及 ν = 0.25。