Hyperelastic Ogden 模型

Ogden 應變能密度函式定義如下：

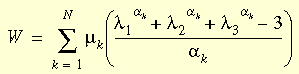
其中：λ_i 是主伸展率，α_i, μ_i 是材料常數，而 N 是函式中的項數，此乃公認為描述橡膠類材料的大幅變形之最佳函式。

Ogden 模型的公式中使用到的罰函數採取 Mooney Rivlin 模型中使用的形式。實際使用的應變能函數則是將 Ogden 函式加以修改後的表達式：

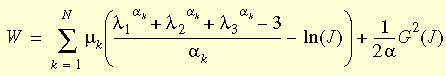
其中 J 是變形量與未變形量的比例，N 是函式中的項數，G(J) = J²-1，且

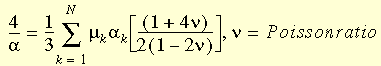
三項式 (經過修改的 Ogden) 模型的運用最為普遍。程式中最多可用到四項式模型 (N=4)。

除了上述的材料常數之外，也需要 Poisson 比。在多數狀況中，只要將 Poisson 比指定在 0.49 到 0.499 的範圍內，即可獲得理想的結果。此外，除非牽涉到大量的體積應變，否則增加 Poisson 比並不會對數值運算結果造成重大影響。

當 Poisson 比幾近於 0.5 時，會因為勁度矩陣中產生負對角項或缺乏收斂性，而導致求解終止。