В связи с обычным применением материала нитинол из-за способности подвергаться конечным напряжениям, для данной модели, применяется теория больших напряжений с использованием логарифмических напряжений вместе с обновленной формулировкой Лагранжа.
Следовательно, модель состояния создается, для отображения отношения логарифмических напряжений и компонентов напряжения Кирхгофа. Однако, в конечном счете, матрица состояния и вектор напряжения трансформируются, для представления напряжений Коши (истинных).

|
σst1, σft1
|
Начальный и конечный пределы текучести для нагрузки растяжения [SIGT_S1, SIGT_F1]
|
|
σst2, σft2
|
Начальный и конечный пределы текучести для разгрузки растяжения [SIGT_S1, SIGT_F1]
|
|
σsc1, σfc1
|
Начальный и конечный пределы текучести для нагрузки сжатия [SIGT_S1, SIGT_F1]
|
|
σsc2, σfc2
|
Начальный и конечный пределы текучести для разгрузки сжатия [SIGT_S1, SIGT_F1]
|
|
eul
|
(Предел прочности при пластичном растяжении) *(3/2)0,5
|
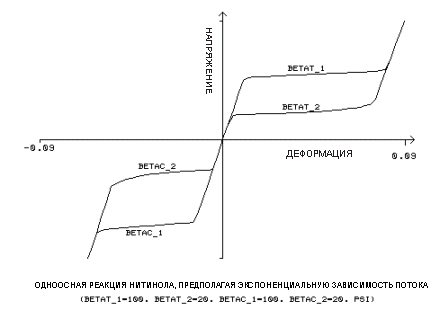
Правило экспоненциального потока использует дополнительные вводные постоянные β
t1, β
t2, β
c1, β
c2:
|
βt1
|
параметр материала, измеряющий скорость изменения нагрузки растяжения, [BETAT_1]
|
|
βt2
|
параметр материала, измеряющий скорость изменения разгрузки растяжения, [BETAT_2]
|
|
βc1
|
параметр материала, измеряющий скорость изменения нагрузки сжатия, [BETAC_1]
|
|
βc2
|
параметр материала, измеряющий скорость изменения разгрузки сжатия, [BETAC_2]
|
Критерий растяжения
Для моделирования возможности зависимости фазовых превращений от давления, используется функция нагрузки по Drucker-Prager для критерия растяжения:
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RIf = 0
Где:
σ(bar) = эффективное напряжение
p = среднее напряжение (или гидростатической давление)
α = sqrt(2/3) (σsc1 - σst1 ) / (σsc1 - σst1)
RfI = [ σfI(sqrt(2/3) + α)], I = 1 для нагрузки и 2 для разгрузки