The n x n symmetric damping matrix [C] is formulated as a linear combination of the mass [M] and stiffness [K] matrices:
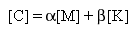(Equation 1)
- Alpha Coefficient: Sets the mass-proportional coefficient α.
- Beta Coefficient: Sets the stiffness-proportional coefficient β.
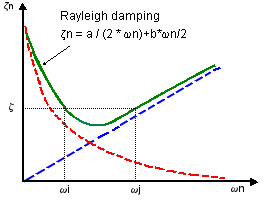
The type of damping described by (Equation 1) is known as Rayleigh or proportional damping.
This form of [C] is orthogonal with respect to the system eigenvectors.
By applying the modal coordinate transformation, the modal damping matrix [c] becomes diagonal:
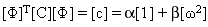(Equation 2)
You can define Rayleigh damping for linear and nonlinear dynamic studies.
Relation of Rayleigh Coefficients and Modal Damping Ratio
The modal damping matrix [c] is given by:
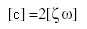(Equation 3)
The coefficient of viscous damping ci for the ith mode is calculated by:
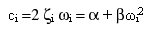(Equation 4),
and the viscous damping ratio ζi is expressed as
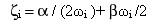(Equation 5)
If the damping ratios for the ith and jth modes are ζi and ζj, then the Rayleigh coefficients α and β are calculated from the solution of the two algebraic equations:
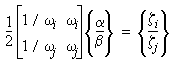(Equation 6)
If both modes have the same damping ratio ( ζi = ζj = ζ) , then the values of α and β are given by:
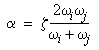(Equation 7) 
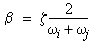(Equation 8)
The viscous damping ratio ζ for any other mode varies with frequency as shown in the figure:
