İçindekiler'i Gizle

Creep Model

Creep is a time dependent strain produced under a state of constant stress.

Creep is observed in most engineering materials especially metals at elevated temperatures, high polymer plastics, concrete, and solid propellant in rocket motors. Since creep effects take long time to develop, they are usually neglected in dynamic analysis.

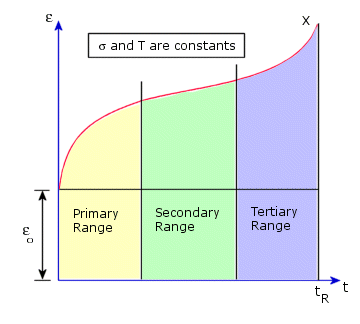
The creep curve is a graph between strain versus time. Three different regimes can be distinguished in a creep curve; primary, secondary, and tertiary. Usually primary and secondary regimes are of interest.

fig_6.gif

Two creep laws based on an “Equation of State” approach are implemented. Each law defines an expression for the uniaxial creep strain in terms of the uniaxial stress and time.

Classical Power Law for Creep (Bailey-Norton law)

36.gif

where:

T = Temperature (Kelvin) (= input temperature + reference temperature + offset temperature)

CT = A material constant defining the creep temperature-dependency

C0 is the Creep Constant 1 you enter in the Properties tab of the Material dialog box.

The units of the Creep Constant 1 must be entered in the SI unit system. The conversion factor is equal to 1/ (stress ^ (C1) * time^(C2)). The stress units are in N/m2 and time is in seconds.

C1 is the Creep constant 2, and C2 is the Creep constant 3 in the material properties dialog box.

The classical power law for creep represents primary and secondary creep regimes in one formula. Tertiary creep regime is not considered. “t” is the current real (not pseudo) time and sigma is the total uniaxial stress at time t.

To extend these laws to multiaxial creep behavior, the following assumptions are made:
  • The uniaxial creep law remains valid if the uniaxial creep strain and the uniaxial stress are replaced by their effective values.
  • Material is isotropic
  • The creep strains are incompressible

For a numerical creep analysis, where cyclic loading may be applied, based on the strain hardening rule, the current creep strain rates are expressed as a function of the current stress and the total creep strain:

38.gif
creep_stress: effective stress at time t
Effective creep strain:total effective creep strain at time t
deviatoric stress tensor: components of the deviatoric stress tensor at time t


Bu başlık hakkında geribildirimde bulunun

SOLIDWORKS; dokümantasyonun sunumu, doğruluğu ve bütünlüğü hakkında geribildiriminizi almaktan memnuniyet duyar. Bu başlık ile ilgili yorum ve önerilerinizi, aşağıdaki formu kullanarak doğrudan dokümantasyon takımımıza yollayın. Dokümantasyon takımı teknik destek sorularına yanıt veremez. Teknik destek ile ilgili bilgiler için buraya tıklayın.

* Gerekli

 
*Email:  
Konu:   Yardım Başlıkları Hakkında Geribildirim
Sayfa:   Creep Model
*Yorum:  
*   Kişisel Bilgilerimin Dassault Systèmes tarafından kullanılacağının belirtildiği gizlilik politikasını okuduğumu ve kabul ettiğimi onaylıyorum

Yazdırma Başlığı

Yazdırılacak içeriğin kapsamını seçin:

x

Internet Explorer 7'den daha eski bir tarayıcı sürümünü kullandığınızı tespit ettik. Optimize edilmiş görünüm için tarayıcınızı Internet Explorer 7 veya daha yenisine yükseltmenizi öneririz.

 Bu mesajı bir daha asla gösterme
x

Web Yardım İçerik Sürümü: SOLIDWORKS 2013 SP05

SOLIDWORKS içindeki Web yardımını devre dışı bırakmak ve onun yerine yerel yardımı kullanmak için Yardım > SOLIDWORKS Web Yardımını Kullan öğelerine tıklayın.

Web yardımı arabirimi ve araması ile ilgili karşılaştığınız sorunları lütfen yerel destek temsilcinize bildirin. Yardım başlıkları hakkında ayrı ayrı geri bildirimde bulunmak için ilgili başlığın sayfasından "Bu başlık hakkında geribildirim" bağlantısına tıklayın.

0.20.21